Двоичная система счисления чисел была изобретена еще до нашей эры. Однако в наши дни, благодаря повсеместному распространению компьютеров и программного двоичного кода, эта система получила второе возрождение. Бинарное представление чисел с помощью всего двух цифр 0 и 1 изучают школьники на уроке информатики. Именно двоичное представление числа «понимают» все компьютеры. Перевод в двоичную систему из любой другой подробно расписан с помощью разных методов. Самым простым считается способ разложения по степеням на основание 2.
Если исходное число представлено в десятичнойсистеме, для его перевода воспользуйтесь методом деления на основание 2. Для этого поделите число на 2 и запишите образовавшийся остаток при делении нацело. Если после деления полученное частное оказалось больше двух, снова поделите его на 2 и также сохраните полученный остаток.
2
Продолжайте итерации деления до тех пор, пока частное окажется меньше 2. После этого запишите ряд полученных в остатках цифр и заключительное частное, начиная с последней итерации. Данная запись из 0 и 1 и будет являться двоичным представлением исходного числа.
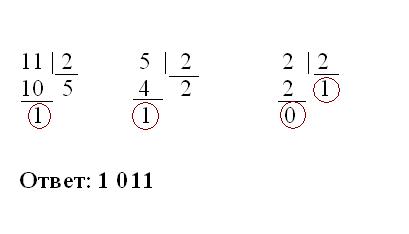
3
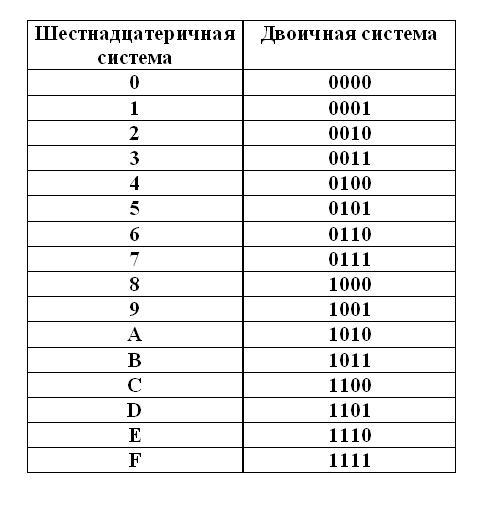
Если заданное число представлено в шестнадцатеричной системе, для его перевода в бинарный вид воспользуйтесь таблицей переходов. В ней каждому числу от 0 до F шестнадцатеричной системы противопоставляется четырехзначный набор цифр в бинарном коде.
4
Так, если вы имеете запись вида: 4ВЕ2, то для ее перевода следует каждый символ заменить на соответствующий набор цифр из таблицы перехода. Порядок записи числа при этом строго сохраняется. Таким образом, цифра 4 из шестнадцатеричной системы заменится на 0100, В – 1011, Е – 1110 и 2 – 0010. И исходное число 4ВЕ2 в бинарной записи будет иметь вид: 0100101111100010.
Видео по теме
Источники:
Как число 1000 в троичной системе перевести в двоичную
