Инструкция
1
Основных операций всего две: перевод из десятичной системы счисления в другую (двоичную, восьмеричную и т.п.) и обратно. Название каждой системы счисления происходит от ее основания - это количество элементов в ней (двоичная - 2, десятичная - 10). В системах счисления с основанием больше 10 принято использовать далее в качестве замены двухзначных чисел буквы латинского алфавита (А - 10, B - 11 и т.д.).
2
Операции рассмотрим на примере двоичной системы счисления, как наиболее распространенной. Для всех других систем будут верны те же правила и методы с точностью до замены основания 2 на соответствующее.
Итак, у нас есть некоторое число в двоичной системе счисления, состоящее из нескольких цифр. Записываем его в виде суммы произведений его цифр, умноженных на 2. Далее у всех 2 расставляем степени справа налево, начиная с 0. Суммируем. Получившее число и есть искомое.
Пример.
1011=1*(2^3)+0*(2^2)+1*(2^1)+1*(2^0)=8+0+2+1=11.
Итак, у нас есть некоторое число в двоичной системе счисления, состоящее из нескольких цифр. Записываем его в виде суммы произведений его цифр, умноженных на 2. Далее у всех 2 расставляем степени справа налево, начиная с 0. Суммируем. Получившее число и есть искомое.
Пример.
1011=1*(2^3)+0*(2^2)+1*(2^1)+1*(2^0)=8+0+2+1=11.
3
Теперь рассмотрим обратную операцию.
Пусть дано число в десятичной системе. Будем делить его столбиком на основание системы счисления, в которую мы хотим его перевести (в нашем случае это будет 2). Деление продолжаем до самого конца, пока частное не станет меньше основания. Далее, начиная с последнего, записываем все остатки в строчку. Это и будет искомое число.
Пример.
11/2 = 5 остаток 1, 5/2 = 2, остаток 1, 2/2 = 1 остаток 0 => 1011.
Еще один пример приведен на картинке.
Для других оснований операции аналогичны. Не забывайте заменять числа, начиная с 10, в соответствующих системах счисления на латинские буквы! В противном случае получившееся число будет считываться неверно, ведь "10" и "1""0" - это абсолютно разные вещи!
Основание системы счисления, в которой представлено число, указывается в виде индекса внизу у крайней правой цифры числа.
Пусть дано число в десятичной системе. Будем делить его столбиком на основание системы счисления, в которую мы хотим его перевести (в нашем случае это будет 2). Деление продолжаем до самого конца, пока частное не станет меньше основания. Далее, начиная с последнего, записываем все остатки в строчку. Это и будет искомое число.
Пример.
11/2 = 5 остаток 1, 5/2 = 2, остаток 1, 2/2 = 1 остаток 0 => 1011.
Еще один пример приведен на картинке.
Для других оснований операции аналогичны. Не забывайте заменять числа, начиная с 10, в соответствующих системах счисления на латинские буквы! В противном случае получившееся число будет считываться неверно, ведь "10" и "1""0" - это абсолютно разные вещи!
Основание системы счисления, в которой представлено число, указывается в виде индекса внизу у крайней правой цифры числа.
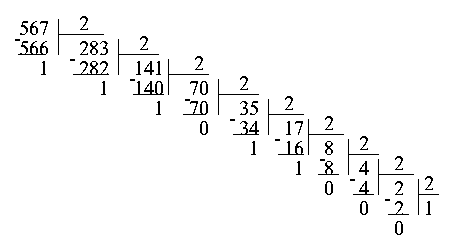
Видео по теме








