Вам понадобится
- - калькулятор.
Инструкция
1
Сначала рассчитайте значения признаков: факторного и результативного (соответственно x и y). Для этого воспользуйтесь формулами средневзвешенной и простой арифметической.
2
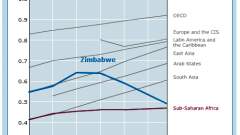
Уравнение регрессии отражает зависимость исследуемого показателя от влияющих на него независимых факторов. Это уравнение нужно найти. Его вид для временного ряда будет представлять собой тренд, характерный для некоей случайной величины, естественно, во времени.
3
В расчетах обычно используется уравнение y=ax+b. Это называется уравнением простой парной регрессии. Хотя реже, но все же применяются и другие уравнения: показательной, экспоненциальной и степенной функций. Что касается типа функции в каждом отдельно взятом случае, определяется он посредством подбора линии, что наиболее точно описывает зависимость, которая исследуется.
4
Чтобы построить линейную регрессию, нужно определить ее параметры. Рассчитывайте их, прибегая к помощи аналитических программ для ПК либо специального калькулятора. Проще всего найти элементы функции, применив классический подход, который основан на методе наименьших квадратов. У признака есть фактические значения и расчетные. Так вот, этот метод заключается в сведении к минимуму суммы квадратов отклонений первых от вторых, а представляет он собой решение системы нормальных уравнений. В ситуации с линейной регрессией формулы, по которым находятся параметры уравнения, таковы:
a = xср – bxср;
b = ((y*x)ср – yср*xср)/(x^2)ср – (xср)^2.
a = xср – bxср;
b = ((y*x)ср – yср*xср)/(x^2)ср – (xср)^2.
5
Составьте теперь на основе полученных вами данных функцию регрессии. Для этого сначала рассчитайте усредненные значения переменных x и y и подставьте их в полученное уравнение. Так вы найдете координаты точек (xi и yi) собственно линии регрессии.
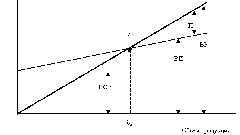
6
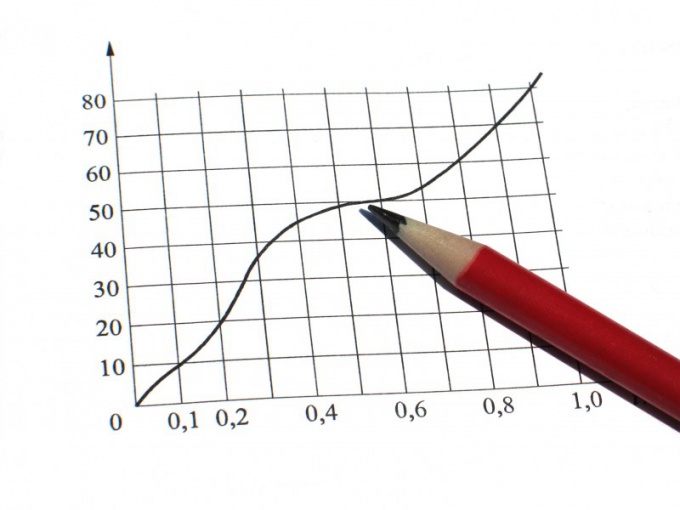
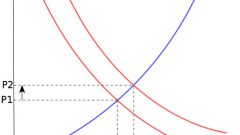
На оси x в прямоугольной системе координат отложите значения xi, на оси y – yi соответственно. Координаты усредненных значений тоже отметьте. В случае, если графики правильно построены, они пересекутся в такой точке, координаты которой будут равняться средним значениям.