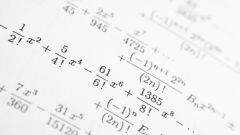Как составить уравнение регрессии

Как врач устанавливает диагноз? Он рассматривает совокупность признаков (симптомов), а затем принимает решение о болезни. На самом деле, он всего лишь делает определенный прогноз, опираясь на некоторую совокупность признаков. Эту задачу легко формализовать. Очевидно, что как установленные симптомы, так и диагнозы в какой-то мере случайны. Именно с такого рода первичных примеров начинается построение регрессионного анализа.

Инструкция

1. Основная задача регрессионного анализа - установление прогнозов о значении какой-либо случайной величины, на основе данных о другой величине. Пусть множество факторов, влияющих на прогноз случайная величина – Х, а множество прогнозов – случайная величина Y. Прогноз должен быть конкретным, то есть необходимо выбрать значение случайной величины Y=y. Это значение (оценка Y=y*) выбирается на основе критерия качества оценки (минимума дисперсии).
2. За оценку в регрессионном анализе принимают апостериорное математическое ожидание. Если плотность вероятности случайной величины Y обозначить p(y), то апостериорная плотность обозначается как p(y|X=x) или p(y|x). Тогда y*=M{Y|=x}=∫yp(y|x)dy (имеется виду интеграл по вcем значениям). Данная оптимальная оценка y*, рассматриваема как функция х, называется регрессией Y на X.
3. Любой прогноз может зависеть от множества факторов, возникает многофакторная регрессия. Однако в данном случае следует ограничиться однофакторной регрессией, помня, что в некоторых случаях набор прогнозов традиционен и может быть рассмотрен как единственный во всей своей совокупности (скажем утро – это восход солнца, окончание ночи, наивысшая точка росы, самый сладкий сон...).
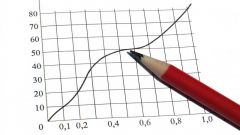
4. Наиболее широкое распространение получила линейная регрессия y=a+Rx . Число R называется коэффициентом регрессии. Реже встречается квадратичная – y= с+bx + ax^2.
5. Определение параметров линейной и квадратичной регрессии можно осуществить с помощью метода наименьших квадратов, который основывается на требовании минимальной суммы квадратов отклонений табличной функции от аппроксимирующей величины. Его применение для линейной и квадратичной аппроксимаций приводит к системам линейных уравнений относительно коэффициентов (см. рис. 1а и 1b):
6. Проводить вычисления «вручную» крайне трудоемко. Поэтому придется ограничиться самым коротким примером. Для практической работы вам потребуется использовать программное обеспечение, предназначенное для расчета минимальной суммы квадратов, которого, в принципе, достаточно много.
7. Пример. Пусть факторы: х1=0, х2=5, х3=10. Прогнозы: y1=2,5, y2=11, y=23. Найти уравнение линейной регрессии. Решение. Составьте систему уравнений (см. рис. 1а) и решите его любым способом.3a+15R=36,5 и 15а+125R=285. R=2,23; a=3,286. y=3,268+2,23.