Инструкция
1
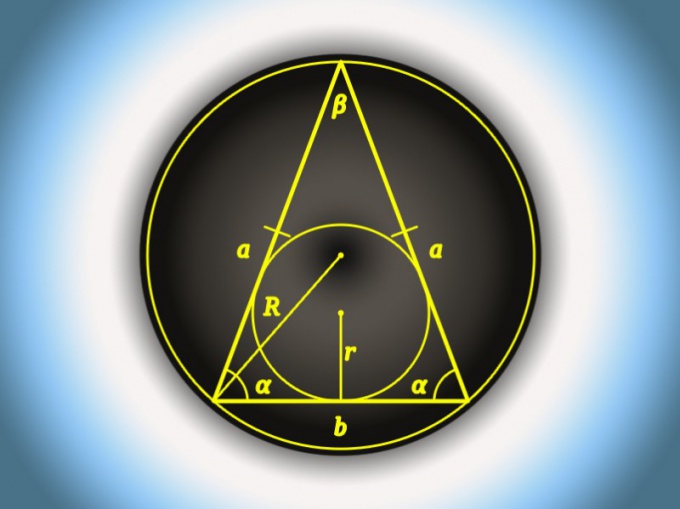
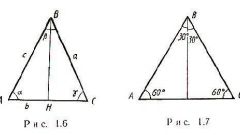
Длину основания (b) равнобедренного треугольника, в котором известна длина боковой стороны (a) и величина угла при основании (α), вычисляйте с использованием теоремы о проекциях. Из нее вытекает, что искомая величина равна двум длинам боковой стороны, умноженным на косинус угла известной величины: b = 2*a*cos(α).
2
Если в условиях предыдущего шага заменить угол, прилежащий к основанию, углом, лежащим напротив него (β), в расчете длины этой стороны (b) можно использовать размер боковой стороны (а) и другую тригонометрическую функцию - синус - от половины величины угла. Эти два значения перемножьте и удвойте: b = 2*a*sin(β/2).
3
Для тех же исходных данных, что и в предыдущем шаге, существует еще одна формула, но она кроме тригонометрической функции включает еще и извлечение корня. Если вас это не пугает, отнимите от единицы косинус угла при вершине треугольника, полученное значение удвойте, извлеките из результата корень и умножьте на длину боковой стороны: b = a*√(2*(1-cos(β)).
4
Зная длину периметра (P) и боковой стороны (a) равнобедренного треугольника найти длину основания (b) очень легко - просто вычтите из первого значения два вторых: b = P-2*a.
5
По значению площади (S) такого треугольника тоже можно рассчитать длину основания (b), если известна высота (h) фигуры. Для этого удвоенную площадь разделите на высоту: b = 2*S/h.
6
Высота (h), опущенная на основание (b) равнобедренного треугольника, может быть использована для вычисления длины этой стороны в сочетании с длиной боковой стороны (a). Если эти два параметра известны, возведите высоту в квадрат, отнимите от полученной величины квадрат длины боковой стороны, из результата извлеките квадратный корень и удвойте: b = 2*√(h²-a²).
7
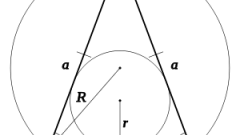
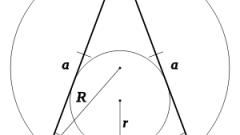
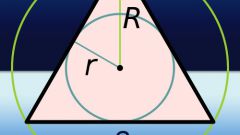
Можно использовать для вычисления длины основания (b) и радиус (R) описанной около треугольника окружности, если известен угол, лежащий напротив основания (β). Двойку умножьте на радиус и синус этого угла: b = 2*R*sin(β).