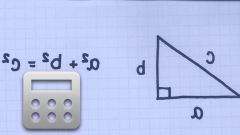Инструкция
1
Самой простой формула расчета площади квадрата (S) будет в том случае, если известна длина стороны (a) этой фигуры - просто умножьте ее на саму себя (возведите в квадрат): S = a².
2
Если в условиях задачи дана длина периметра (P) этой фигуры, к приведенной выше формуле надо добавить еще одно математическое действие. Так как периметр складывается из суммы длин всех сторон многоугольника, в квадрате он содержит четыре одинаковых слагаемых, т.е. длину каждой стороны можно записать как P/4. Подставьте это значение в формулу предыдущего шага. У вас должно получиться такое равенство: S = P²/4² = P²/16.
3
Диагональ квадрата (L) соединяет две его противоположных вершины, образуя вместе с двумя сторонами прямоугольный треугольник. Это свойство фигуры позволяет с использованием теоремы Пифагора (L²=a²+a²) по длине диагонали вычислить длину стороны (a=L/√2). Подставьте и это выражение во все ту же формулу из первого шага. В общем виде решение должно выглядеть так: S = (L/√2)² = L²/2.
4
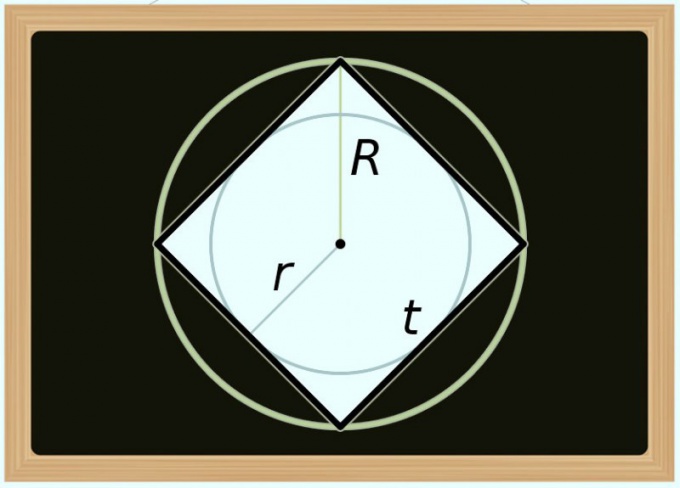
Можно рассчитать площадь квадрата и по диаметру (D) описанной около него окружности. Так как диагональ любого правильного многоугольника совпадает с диаметром описанной окружности, в формуле предыдущего шага замените лишь обозначение диагонали обозначением диаметра: S = D²/2. Если нужно выразить площадь не через диаметр, а через радиус (R), преобразуйте равенство таким образом: S = (2*R)²/2 = 2*R².
5
Вычисление площади по диаметру (d) вписанной окружности немногим сложнее, так как применительно к квадрату эта величина всегда равна длине его стороны. Как и в предыдущем шаге, для получения формулы вычислений вам нужно лишь заменить обозначение в уже описанном выше равенстве - на этот раз задействуйте тождество из первого шага: S = d². При необходимости использовать вместо диаметра радиус (r), трансформируйте эту формулу так: S = (2*r)² = 4*r².
Видео по теме