Инструкция
1
Если известна длина стороны квадрата (t), то для нахождения его периметра (p) просто увеличьте эту величину в четыре раза: p=4*t.
2
Если длина стороны неизвестна, но в условиях задачи дана длина диагонали (c), то этого достаточно для вычисления длины сторон, а следовательно и периметра (p) многоугольника. Используйте теорему Пифагора, которая утверждает, что квадрат длины длинной стороны прямоугольного треугольника (гипотенузы) равен сумме квадратов длин коротких сторон (катетов). В прямоугольном треугольнике, составленном из двух смежных сторон квадрата и соединяющего их крайние точки отрезка, гипотенуза совпадает с диагональю четырехугольника. Из этого вытекает, что длина стороны квадрата равна отношению длины диагонали к квадратному корню из двойки. Используйте это выражение в формуле для вычисления периметра из предыдущего шага: p=4*c/√2.
3
Если дана лишь площадь (S) ограниченного периметром квадрата участка плоскости, то и этого будет достаточно, чтобы определить длину одной стороны. Так как площадь любого прямоугольника равна произведению длин его смежных сторон, то для нахождения периметра (p) извлеките квадратный корень из площади, а результат увеличьте в четыре раза: p=4*√S.
4
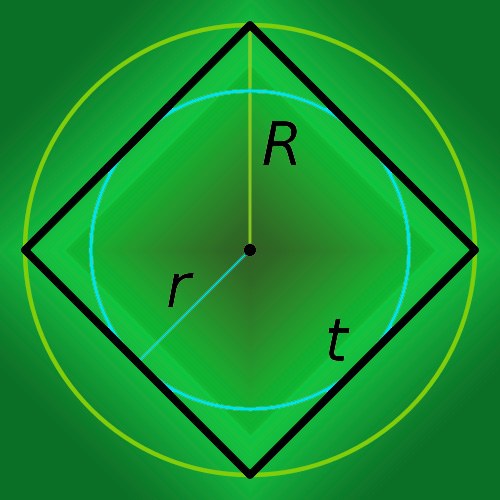
Если известен радиус описанной возле квадрата окружности (R), то для нахождения периметра многоугольника (p) умножьте его на восемь и разделите полученный результат на квадратный корень из двойки: p=8*R/√2.
5
Если окружность, радиус которой известен, вписана в квадрат, то вычисляйте его периметр (p) простым умножением радиуса (r) на восьмерку: P=8*r.
6
Если рассматриваемый квадрат в условиях задачи описан координатами своих вершин, то для вычисления периметра вам понадобятся данные лишь о двух вершинах, принадлежащих к одной из сторон фигуры. Определите длину этой стороны, исходя из все той-же теоремы Пифагора для треугольника, составленного из нее самой и ее проекций на оси координат, а полученный результат увеличьте в четыре раза. Так как длины проекций на координатные оси равны модулю разностей соответствующих координат двух точек (X₁;Y₁ и X₂;Y₂), то формулу можно записать так: p=4*√((X₁-X₂)²+(Y₁-Y₂)²).