Инструкция
1
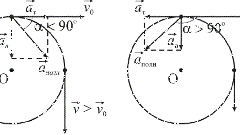
Если некоторое тело разогнать до даже очень большой скорости в вертикальном направлении, то израсходовав запасы кинетической энергии, оно все равно вернется назад. Причина – отсутствие в этом направлении каких-либо сил кроме земного притяжения. Значит должна быть сила, противодействующая силе тяжести. Такая сила имеет место, если тело участвует во вращательном движении относительно Земли (точнее ее центра). При таком движении возникает центростремительное ускорение, создающее силу, направленную противоположно тяготению.
2
Теперь вы вправе сделать вывод о том, что рассматриваемая скорость направлена по касательной к окружности, по которой движется тело. Она называется линейной скоростью вращательного движения. Если масса тела m, то соответствующая центробежная сила Fц=m(v^2/L), где L – расстояние от центра Земли до тела. Если пользоваться высотой h удаления тела от поверхности, то L=R+h (R – радиус Земли).
3
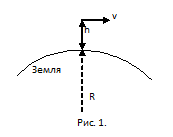
Гравитационная сила притяжения двух масс γ(Mm/L^2)=γ(Mm/(R+h)^2), где γ – гравитационная постоянная. Приравняйте ее центробежной силе (см. рис. 1). Получите γ(Mm/(R+h)^2)= m(v^2/(R+h)). Проведите сокращения и найдите v. v=√(γM/(R+h). Теперь учтите, что h пренебрежимо мало по сравнению с R или R+h≈R. Учтите и то, что ускорение свободного падения g=γМ/R^2. Тогда v=√(gR). R=6357*(10^3) м, g=9,81 м/с^2 и тогда v≈7,91 км/с.
4
Вместе тем, при завершении решения задачи о первой космической скорости не может не возникнуть вопрос о том, как быть с высотой h? Действительно, в окончательном расчете эта величина не участвовала. Дело в том, что даже те высоты, на которых летают околоземные космические аппараты, слишком малы по сравнению с радиусом земли. Да и массы их так же ничтожны в сравнении с массой нашей планеты. Тем не менее, к h остается главное требование. Больше толщины атмосферы. В плотных ее слоях тела с такими скоростями просто сгорают.
Источники:
- Никеров В.Л. Физика. Современный курс. М.: - 2011, 452 с.