Инструкция
1
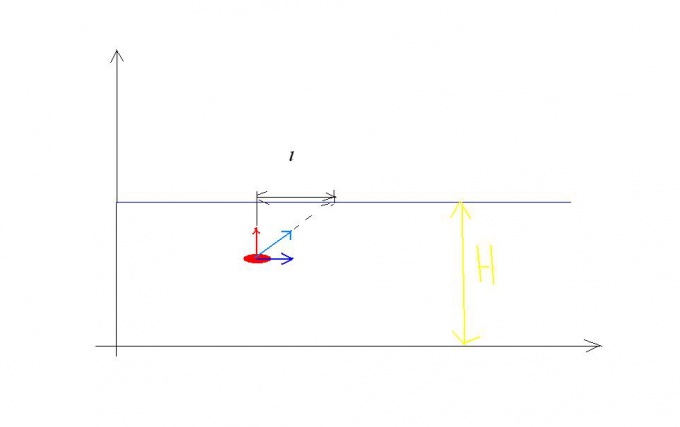
Пример на правило сложения скоростей. Пусть скорость течения реки v0, а скорость лодки, переплывающей эту реку, относительно воды равна v1 и направлена перпендикулярно берегу (см рисунок 1). Лодка одновременно участвует в двух независимых движениях: она за некоторое время t переплывает реку шириной Н со скоростью v1 относительно воды и за это же время ее сносит вниз по течению реки на расстояние l. В результате лодка проплывает путь S со скоростью v относительно берега, равной по модулю: v равно корень квардратный из выражения v1 в квадрате + v0 в квадрате за это же самое время t. Поэтому можно записать уравнения, которые решают подобные задачи: H=v1t, l = v0t? S= корень квадратный из выражения: v1 в квадрате + v0 в квадрате, умноженный на t.
2
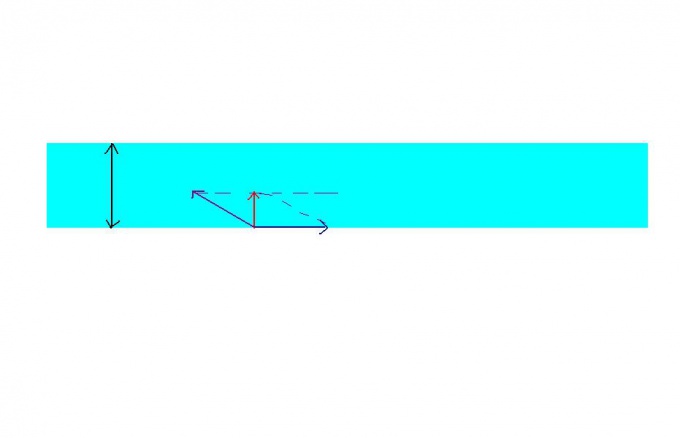
Другой тип таких задач задает вопросы: под каким углом к берегу должне грести гребец в лодке, чтобы оказаться на противоположном берегу, пройдя во время переправы минимальный путь? За какое время этот путь будет пройден? С какой скоростью лодка пройдет этот путь?Чтобы ответить на эти вопросы следует сделать рисунок (см рис 2). Очевидно, что минимальный путь, который может пройти лодка, пересекая реку, равен ширине реки Н. Чтобы проплыть этот путь, гребец должен направить лодку под таким углом а к брегу, при которм вектор абсолютной скорости лодки v будет направлен перпендикулярно берегу. Тогда из прямоугольного треугольника можно найти: cos a=v0/v1. Отсюда можно извлечь угол а. Скорость определить из этого же треугольника по теореме Пифагора: v= корень квадратный из выражения: v1 в квадрате - v0 в квадрате.И наконец время t, за которое лодка пересечет реку шириной Н, двигаясь со скоростью v, будет t=H/v.
Видео по теме
Источники:
- решение задач на течение реки