Инструкция
1
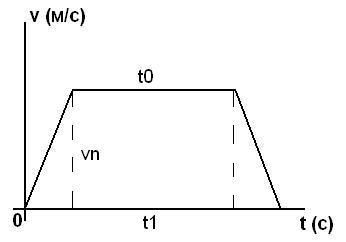
Постройте по данным задачи график зависимости скорости движения тела от времени v(t). Здесь горизонтальная координата представляет собой изменение времени (с), вертикальная – скорости (м/с). Как правило, в задачах рассматривается неравномерное перемещение тел в определенные промежутки времени. Любое изменение скорости на графике будет отображено возрастанием или убыванием. Например, при начале движения тела с постоянным ускорением в течение 20 с его скорость в итоге составила 15 м/с. Отложите на графике прямую, начинающуюся в начале координат (0, 0) и заканчивающуюся в точке (20, 15), где 20 с откладываются вправо по оси времени t, а 15 м/с – вверх по скорости. При наличии равномерного движения тела отобразите его прямой, параллельной горизонтальной оси.
2
Для нахождения средней скорости перемещения нужно знать путь и время, затраченное на движение. Вычислите площадь S под кривой v(t), которая является графическим представлением пройденного телом пути L. Часто график перемещения ограничивает фигуру трапецию. Ее площадь находится по формуле: S = ½*(t0 + t1)*vn, где t0 и t1 – основания трапеции – части графика скорости, vn – высота фигуры, здесь максимальная скорость в пути. Подставьте в формулу известные значения и вычислите результат. Если график v(t) представляет собой не трапецию, ее площадь вычисляется по иным формулам, в зависимости от полученной фигуры.
3
Найдите среднюю скорость движения тела по формуле Vср = L/t. Подставив заданное время перемещения и вычисленный путь, посчитайте числовое значение средней скорости.
4
Среднюю скорость можно вычислить и по графику зависимости пути от времени l(t). Для этого соедините прямой линией начальную и конечную точки рассматриваемого участка перемещения. Средняя скорость тела будет равна тангенсу угла наклона полученной прямой к оси времени.