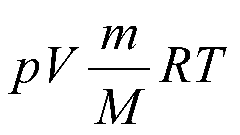Как найти температуру воздуха при постоянном давлении

Всякое изменение состояния газа принято считать термодинамическим процессом. При этом самые простейшие процессы, протекающие в идеальном газе, называют изопроцессами. При изопроцессе масса газа и еще один его параметр (давление, температура или объем) остаются постоянными, остальные же изменяются.

Вам понадобится

• - калькулятор;
• - исходные данные;
• - карандаш;
• - линейка;
• - ручка.

Инструкция

1. Изопроцесс, в котором давление остается постоянным, называется изобарным. Существующая зависимость между объемом газа и его температурой при постоянном давлении этого газа была установлена опытным путем французским ученым Л. Гей Люссаком в 1808 году. Он показал, что объем идеального газа при постоянном давлении увеличивается с возрастанием температуры. Другими словами, объем газа прямо пропорционален его температуре при условии постоянного давления.
2. Описанная выше зависимость была выражена в формуле: Vt = V0(1 + αt), где V0 – объем газа при температуре нуль градусов, Vt – объем газа при температуре t, которая измерена по шкале Цельсия, α – величина термического коэффициента объемного расширения. Абсолютно для всех газов α = (1/273°С–1). А значит, Vt = V0(1 + (1/273)t). Отсюда, t = (Vt - V0)/((1/273)/V0).
3. Подставьте в эту формулу исходные данные и подсчитайте значение температуры при постоянном давлении для идеального газа.
4. Обратите внимание на то, что полученный результат справедлив лишь для идеального газа. Реальные газы подчинены данной зависимости лишь в достаточно разреженном состоянии, то есть, когда показатели давления воздуха и его температуры не имеют критического значения, при котором начинается процесс сжижения газа. Давление большинства газов при комнатной температуре изменяет от 10 до 102 атмосфер.
5. Графически изобразите зависимость температуры, давления и объема воздуха. Так, график зависимости объема и температуры будет выглядеть в виде прямой, которая выходит из точки Т=0. Данная прямая называется изобарой.