Инструкция
1
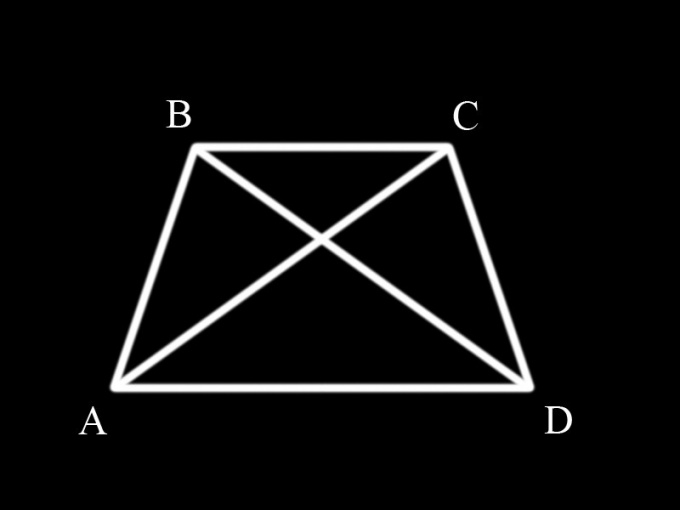
Для начала необходимо вспомнить, что такое трапеция и какими свойствами она обладает. Трапеция – это четырехугольник, две противоположные стороны которого параллельны. Параллельные стороны являются основаниями трапеции, а две другие – ее боковыми сторонами. Если боковые стороны трапеции равны, то она называется равнобочной. Углы при основаниях равнобочной трапеции попарно равны, т.е. угол АВС равен углу ВСD, а угол ВАD равен углу СDА.
2
Диагонали делят трапецию на треугольники. Для доказательства равенства диагоналей равнобочной трапеции необходимо рассмотреть треугольники АВС и ВСD и доказать, что они равны между собой, поскольку диагонали АС и ВD одновременно являются сторонами данных треугольников.
3
Сторона АВ треугольника АВС равна стороне СD треугольника ВСD, поскольку они являются одновременно боковыми сторонами равнобочной трапеции (т.е. по условию). Угол АВС треугольника АВС равен углу ВСD треугольника ВСD, поскольку они являются углами, лежащими при основании трапеции (свойство равнобочной трапеции). Сторона ВС является общей для обоих треугольников.
4
Таким образом, имеется два треугольника с двумя равными сторонами и равными углами, заключенными между ними. Следовательно треугольник АВС равен треугольнику ВСD по первому признаку равенства треугольников.
5
Если треугольники равны, то равны и их соответствующие стороны, т.е. сторона АС равна стороне ВD и, поскольку они одновременно являются диагоналями равнобочной трапеции, их равенство доказано.
6
Для доказательства можно использовать треугольники АВD и АСD, которые также равны между собой по первому признаку равенства треугольников. В этом случае доказательство аналогично.
7
Утверждение, что диагонали равны, справедливо только для равнобочной трапеции.
Видео по теме