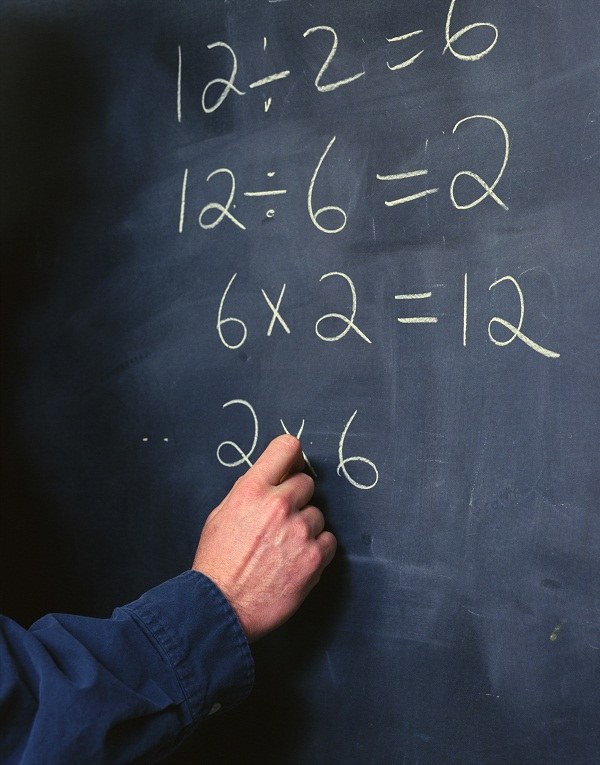Почему нельзя делить на ноль

Делить на ноль нельзя, это известно каждому школьнику, но многим совершенно неясно почему. Причины этого правила можно узнать только в высшем учебном заведении, и то только если вы будете изучать математику. В действительности, основание того, что на ноль делить нельзя, не такое уж сложное. Выяснить это было бы очень интересно многим школьникам.

Причина того, что нельзя делить на ноль, лежит в математике. В то время как в арифметике есть четыре основные операции над числами (это сложение, вычитание, умножение и деление), в математике таких только две из них (это сложение и умножение). Именно они включены в определение числа. Чтобы определить, что такое вычитание и деление, нужно воспользоваться сложением и умножением и вывести новые операции из них. Чтобы понять этот момент, полезно рассмотреть несколько примеров. Например, операция 10-5, с точки зрения ученика школы, означает, что от числа 10 отнимается число 5. Но математика ответила бы на вопрос о том, что здесь происходит, иначе. Данная операция была бы сведена к уравнению x+5=10. Неизвестное в данной задаче это x, именно оно и является результатом так называемого вычитания. С делением все происходит аналогично. Оно всего лишь точно также выражается через умножение. При этом, результат – это просто подходящее число. Например, 10:5 математик записал бы как 5*x=10. Данная задача имеет однозначное решение. Учтя все это, можно понять, почему нельзя делить на ноль. Запись 10:0 превратилась бы в 0*x=10. То есть, результатом стало бы число, которое при умножении на 0 дает другое число. Но всем известно правило о том, что любое число, умноженное на ноль, дает ноль. Это свойство включено в понятие о том, чем является ноль. Поэтому получается, что задача о том, как разделить число на ноль, не имеет решения. Это нормальная ситуация, немало задач в математике не имеют решения. Но как может показаться, из этого правила есть одно исключение. Да, ни одно число нельзя делить на ноль, но ведь сам ноль можно? Например, 0*x=0. Это ведь верное равенство. Но проблема в том, что на месте x может быть совершенно любое число. Поэтому результатом такого уравнения стала бы совершенная неопределенность. Нет причин предпочесть какой-либо один результат. Поэтому ноль на ноль делить тоже нельзя. Правда, в математическом анализе с подобными неопределенностями умеют справляться. Выясняют, нет ли в задаче дополнительных условий, благодаря которым становится возможным «раскрыть неопределенность» - так это называется. Но в арифметике так не делают.