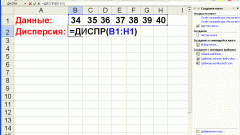
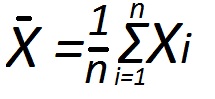Вам понадобится
- - бумага;
- - ручка.
Инструкция
1
Для рассмотрения данного вопроса необходимо ввести некоторые обозначения. Возведение в степень будет обозначено через символ «^», корень квадратный – «sqrt», а обозначения, которые касаются интегралов, приведены на рис.1.
2
Пусть известно среднее значение (математическое ожидание) mx случайной величины (СВ) Х. следует напомнить, что операторное обозначение математического ожидания mх=М{X} =M[X], при этом для него справедливо свойство M{aX} = aM{X}. Математическое ожидание константы есть сама эта константа (М{a}=a). Кроме того, необходимо ввести понятие центрированной СВ. Хц =Х-mx. Очевидно, M{XЦ}=M{X} –mx=0
3
Дисперсией СВ (Dх) называют математическое ожидание квадрата центрированной СВ. Dх=int((x-mx)^2)W(x)dx). При этом W(x) - плотность вероятности СВ. Для дискретных СВ Dх=(1/n)((x- mx)^2 +(x2- mx)^2+…+(xn- mx)^2). Для дисперсии, как и для математического ожидания, предусмотрена операторная запись Dх=D[X] (или D{X}).
4
Из определения дисперсии вытекает, что аналогичным образом ее можно найти по следующей формуле: Dx=M{(X- mx)^2}=D{X}=М{Xц^2}.На практике в качестве примера характеристики рассеивания чаще пользуются средним квадратом отклонения СВ (СКО - среднеквадратическое отклонение). бх=sqrt(Dx), при этом размерность Х и СКО совпадают [X]=[бх].
5
Свойства дисперсии.1. D[a]=0. Действительно, D[a]=M[(a-a)^2]=0 (физический смысл - у постоянной величины нет разброса).2. D[aX]=(a^2)D[X], так как М{(aX-M[aX])^2}=M{(aX - (amx))^2}=(a^2)M{(X - mx)^2}=(a^2)D{X}.3. Dx= M{X^2}-(mx^2), т.к. M{(X - mх)^2}=M{X^2 - 2Xmx + mx^2}=M{X2} - 2M{X}mx + mx2==M{X^2} - 2mx^2+mx^2=M{X^2} – mx^2.4. Если СВ X и Y независимы, то M{XY}=M{X}M{Y}.5. D{X+Y}=D{X-Y}=D{X}+D{Y}. Действительно, учитывая что Х и Y независимы, независимыми являются и Хц и Yц. Тогда, например, D{X-Y}=M{((X-Y)-M[X-Y])^2}=M{((X-mx)+(Y-my))^2}=M{Xц^2}+M{Yц^2}-М{Xц^2}M{Yц^2}=DxDy.
6
Пример. Дана плотность вероятности случайного напряжения Х (см рис.2). Найти ее дисперсию и СКО.Решение. По условию нормировки плотности вероятности, площадь под графиком W(x) равна 1. Так как это треугольник, то (1/2)4W(4)=1. Тогда W(4)=0,5 1/B. Отсюда W(x)=(1/8)x. mx=int(0 – 4)(x(x/8)dx==(x^3)/24|(0 – 4)=8/3. При вычислении дисперсии удобнее всего использовать ее 3-е свойство: Dx= M{X^2}-(mx^2)=int(0 – 4)((x^2)(x|8)dx - 64|9=(x^4)/32)|(0 – 4)-64/9= 8-64/9=8/9.