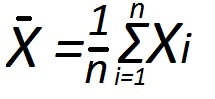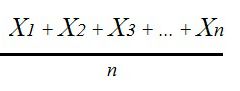Инструкция
1
Сначала стоит разобраться в том, как образуется эта самая выборочная средняя. Допустим, дана какая-то совокупность из числовых значений, которая состоит из n единиц. Все эти единицы образуют так называемую выборку. Сумма всех этих чисел будет формулой выражаться как ΣXi (Xi - это какое-либо из значений этой выборки, где i = 1,2,3...i-1,i. То есть i - это номер значения из выборки). Тогда, для того чтобы найти выборочную среднюю, необходимо сложить все значения из данной выборки и поделить на их количество n.
2
Все записанные сверху данные можно выразить одной лишь формулой, которая указана выше. Выборочная средняя - это самая простая из характеристик, раскрывающих сущность выборочной совокупности. Она широко применяется в математической статистике, теории вероятностей, а также и во многих других областях знания.
3
В школьной программе не дается каких-либо формул для нахождения детей на уроке математики в 5 классе просят найти среднее значение каких либо чисел, то дети уже знают, что, для того чтобы найти среднее значение этих чисел, им понадобится сложить их все, а затем поделить на их число. Фактически они тоже находят выборочную среднюю.
Обратите внимание
Когда смотришь на формулу выборочной средней, то сразу же вспоминается курс школьной математики, в котором нужно было находить среднюю арифметическую. Действительно, формулы практически идентичны, но с математической точки зрения при нахождении выборочной средней рассматривается не какая-то заданная уже совокупность (как это было дано в задачнике по математике), а пространство, в котором существует множество произвольных значений. Исследуя это пространство, находится какая-то выборочная совокупность, из которой впоследствии и находится выборочная средняя.