Как вычислить дисперсию и математическое ожидание

Дисперсия и математическое ожидание являются основными характеристиками случайного события при построении вероятностной модели. Эти величины связаны между собой и в совокупности представляют основу для статистического анализа выборки.

Инструкция

1. Любая случайная величина обладает целым рядом числовых характеристик, определяющих ее вероятность и степень отклонения от истинного значения. Это начальные и центральные моменты разного порядка. Первый начальный момент называется математическим ожиданием, а центральный момент второго порядка – дисперсией.
2. Математическое ожидание случайной величины представляет собой ее среднее ожидаемое значение. Также эту характеристику называют центром распределения вероятностей и находят путем интегрирования по формуле Лебега-Стильтьеса:m = ∫xdf(x), где f(x) – функция распределения, значениями которой являются вероятности элементов множества x ∈ X.
3. Исходя из начального определения интеграла функции, математическое ожидание можно представить в виде интегральной суммы числового ряда, члены которого состоят из пар элементов множеств значений случайной величины и ее вероятностей в этих точках. Пары связаны операцией умножения: m = Σxi•pi, интервал суммирования составляет i от 1 до ∞.
4. Приведенная формула является следствием из интеграла Лебега-Стильтьеса для случая, когда анализируемая величина X дискретная. Если же она целочисленная, то вычислить математическое ожидание можно через производящую функцию последовательности, которая равна первой производной функции распределения вероятностей при x=1:m = f’(x) = Σk•p_k при 1 ≤ k

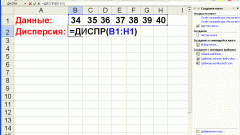
   Дисперсия случайной величины используется для оценки среднего значения квадрата ее отклонения от математического ожидания, а точнее - ее разброса вокруг центра распределения. Таким образом, эти две величины оказываются связанными формулой:d = (x - m)² .

   
   

   Подставив в нее уже известное представление математического ожидания в виде интегральной сумме, можно вычислить дисперсию следующим образом:d = Σpi•(xi - m)².
5. Дисперсия случайной величины используется для оценки среднего значения квадрата ее отклонения от математического ожидания, а точнее - ее разброса вокруг центра распределения. Таким образом, эти две величины оказываются связанными формулой:d = (x - m)² .
6. Подставив в нее уже известное представление математического ожидания в виде интегральной сумме, можно вычислить дисперсию следующим образом:d = Σpi•(xi - m)².