Инструкция
1
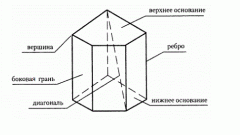
Основаниями прямой призмы являются равные друг другу многоугольники. Боковые ребра призмы соединяют вершины верхнего и нижнего многоугольника и перпендикулярны плоскостям оснований. Следовательно, боковые грани прямой призмы являются прямоугольниками. Эти прямоугольники образованы каждый двумя боковыми ребрами призмы и двумя сторонами фигуры основания (верхнего и нижнего).
2
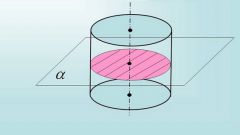
Сечение призмы плоскостью, параллельной основаниям, образует фигуру, равную основанию. Все стороны такого сечения известны или определяются в процессе решения многоугольника.
3
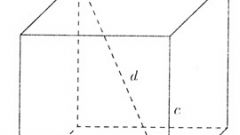
Сечение призмы плоскостью, перпендикулярной основаниям, образует в пределах многогранника прямоугольник. Две стороны прямоугольника в этом сечении равны боковым ребрам призмы. Две другие стороны сечения лежат в плоскостях оснований и являются диагоналями многоугольников, если соединяют вершины фигуры оснований. Либо рассматриваемые стороны сечения могут соединять произвольные точки на сторонах многоугольника. Тогда для их нахождения необходимо провести в многоугольнике основания вспомогательные линии так, чтобы искомая сторона сечения стала стороной треугольника, в две другие стороны являются сторонами основания призмы. Нахождение неизвестной стороны сечения сводится к решению треугольника.
4
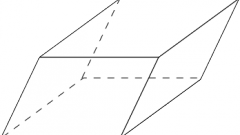
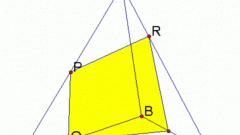
Сечение призмы плоскостью, расположенной под произвольным углом к основаниям и пересекающей плоскости оснований за пределами многогранника, является многоугольником с числом сторон, равным числу сторон основания. Каждую сторону образовавшейся в сечении фигуры нужно находить отдельно. Искомые стороны этого произвольного сечения делят каждую боковую грань прямой призмы на две прямоугольные трапеции. Отрезки боковых ребер призмы являются параллельными основаниями трапеций, сторона основания в трапеции является стороной и одновременно высотой. Искомая сторона сечения в каждой трапеции является четвертой стороной. Таким образом, задача нахождения сторон сечения прямой призмы произвольной наклонной плоскостью сводится к вычислению стороны прямоугольной трапеции.
Видео по теме