Вам понадобится
- Калькулятор, лист бумаги и карандаш (ручка)
Инструкция
1
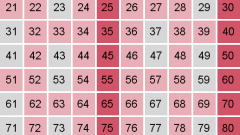
Способ 1. Решето Эратосфена.
По этому методу, чтобы найти все простые числа не больше определенного значения Х, необходимо выписать подряд все целые числа от одного до Х. Возьмем число 2 как первое простое число. Вычеркнем из списка все числа, делящиеся на 2. Затем возьмем следующее после двойки, не вычеркнутое число, и вычеркнем из списка все числа, делящиеся на взятое нами число. И далее каждый раз будем брать следующее не вычеркнутое число и вычеркивать из списка все числа, делящиеся на взятое нами число. И так до тех пор пока выбранное нами число не станет больше, чем Х/2. Все оставшиеся в списке не вычеркнутые числа являются простыми
По этому методу, чтобы найти все простые числа не больше определенного значения Х, необходимо выписать подряд все целые числа от одного до Х. Возьмем число 2 как первое простое число. Вычеркнем из списка все числа, делящиеся на 2. Затем возьмем следующее после двойки, не вычеркнутое число, и вычеркнем из списка все числа, делящиеся на взятое нами число. И далее каждый раз будем брать следующее не вычеркнутое число и вычеркивать из списка все числа, делящиеся на взятое нами число. И так до тех пор пока выбранное нами число не станет больше, чем Х/2. Все оставшиеся в списке не вычеркнутые числа являются простыми
2
Способ 2. Решето Сундарама.
Из ряда натуральных чисел от 1 до N исключаются все числа вида
х + у + 2ху,
где индексы х (не больший у) пробегают все натуральные значения, для которых х+у+2ху не больше N, а именно значения х=1, 2,...,((2N+1)1/2-1)/2 и х=у, х+1,...,(N-х)/(2х+1)ю. Затем каждое из оставшихся чисел умножается на 2 и увеличивается на 1. Полученная в результате последовательность представляет собой все нечётные простые числа в ряду от одного до 2N+1.
Из ряда натуральных чисел от 1 до N исключаются все числа вида
х + у + 2ху,
где индексы х (не больший у) пробегают все натуральные значения, для которых х+у+2ху не больше N, а именно значения х=1, 2,...,((2N+1)1/2-1)/2 и х=у, х+1,...,(N-х)/(2х+1)ю. Затем каждое из оставшихся чисел умножается на 2 и увеличивается на 1. Полученная в результате последовательность представляет собой все нечётные простые числа в ряду от одного до 2N+1.
3
Способ 3. Решето Аткина.
Решето Аткина представляет собой сложный современный алгоритм нахождения всех простых чисел до заданного значения Х. Основная суть алгоритма состоит в представлении простых чисел как целых с нечетным числом представлений в данных квадратных формах. Отдельный этап алгоритма отсеивает числа, кратные квадратам простых чисел в интервале от 5 до Х.
Решето Аткина представляет собой сложный современный алгоритм нахождения всех простых чисел до заданного значения Х. Основная суть алгоритма состоит в представлении простых чисел как целых с нечетным числом представлений в данных квадратных формах. Отдельный этап алгоритма отсеивает числа, кратные квадратам простых чисел в интервале от 5 до Х.
4
Тесты простоты.
Тесты простоты-- это алгоритмы, позволяющие определить, является ли конкретное число Х простым.
Один из самых простых, но и трудоемких тестов-- это перебор делителей. Он состоит в преборе всех целых чисел от 2 до квадратного корня из Х и в вычислении остатка от деления Х на каждое из этих чисел. Если остаток от деления числа Х на некоторое число (больше 1 и меньше Х) равен нулю, то число Х является составным. Если выявляется, что число Х невозможно сократить без остатка ни на одно из чисел, кроме единицы и самого себя, то число Х простое.
Кроме этого способа существует также большое количество других тестов для тестирования простоты числа. Большинство этих тестов являются вероятностными и используются в криптографии. Единственный тест, гарантирующий получение ответа (тест AKS) очень сложен в вычислении, что затрудняет его практическое применение
Тесты простоты-- это алгоритмы, позволяющие определить, является ли конкретное число Х простым.
Один из самых простых, но и трудоемких тестов-- это перебор делителей. Он состоит в преборе всех целых чисел от 2 до квадратного корня из Х и в вычислении остатка от деления Х на каждое из этих чисел. Если остаток от деления числа Х на некоторое число (больше 1 и меньше Х) равен нулю, то число Х является составным. Если выявляется, что число Х невозможно сократить без остатка ни на одно из чисел, кроме единицы и самого себя, то число Х простое.
Кроме этого способа существует также большое количество других тестов для тестирования простоты числа. Большинство этих тестов являются вероятностными и используются в криптографии. Единственный тест, гарантирующий получение ответа (тест AKS) очень сложен в вычислении, что затрудняет его практическое применение