Инструкция
1
Согласно основной теореме арифметики, любое натуральное число, которое больше единицы, может быть разложено на произведение простых чисел. Исходя из этого, можно сделать вывод о том, что простые числа представляют собой определенные «блоки» для натуральных чисел.
2
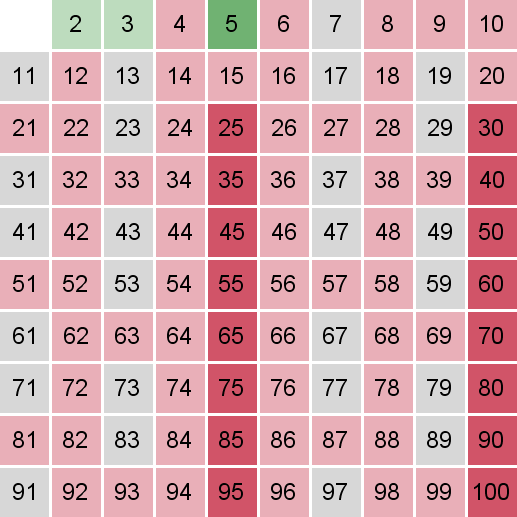
Операцию представления натурального числа в виде произведения простых называют факторизацией или разложением на простые множители. Полиномиальные алгоритмы разложения чисел неизвестны, но также нет доказательств того, что в природе они не существуют.
3
На сложности вычислений, связанных с факторизацией чисел, основаны некоторые криптосистемы, например, одной из известных является RSA. Для квантовых компьютеров существует алгоритм Шора, который позволяет осуществлять факторизацию чисел с полиномиальной сложностью.
4
Существуют алгоритмы, с помощью которых можно осуществлять поиск, а также распознавать простые числа. Самыми простыми из них являются решето Эратосфена, решето Аткина, решето Сундарама. На деле же часто встает задача не получения простых чисел, а проверки числа на то, является ли оно простым. Алгоритмы, призванные решать подобные задачи, именуются тестами простоты.
5
Еще Евклидом был доказан тот факт, что простых чисел существует бесконечно много. Суть его доказательства, представленного в книге «Начала», заключается в следующем. Пусть существует конечное число простых чисел. Перемножим их, после чего прибавим к ним единицу. Число, которое получилось, не может быть разделено ни на какое простое число из конечного набора без остатка (он будет равен 1). В таком случае это число делится на простое число, которое не входит в состав представленного конечного набора. Помимо этого, существуют также и другие математические доказательства бесконечности простых чисел.
Видео по теме
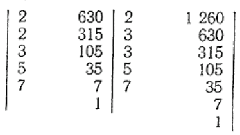




сумма нечетных цифр числа 121 = 1+1 = 2
сумма его четных цифр тоже = 2
разность их = 0
делится ли 0 на 11?