Как рассчитать достоверность

Чтобы сравнить две выборки, взятые из одной генеральной совокупности, либо два различных состояния одной и той же совокупности, используется метод Стьюдента. С его помощью можно рассчитать достоверность различий, то есть узнать, можно ли доверять проведенным измерениям.

Инструкция

1. Для того чтобы правильно выбрать формулу расчета достоверности, определите величину групп выборок. Если количество измерений больше 30, такая группа будет считаться большой. Таким образом, возможно три варианта: обе группы малые, обе группы большие, одна группа малая, вторая – большая.
2. Кроме того, вам понадобится знать, зависимы ли измерения первой группы с измерениями второй. Если каждая i-ая варианта первой группы противопоставлена i-ой варианте второй группы, то они называются попарно-зависимыми. Если же варианты внутри группы можно менять местами, такие группы называются группами с попарно-назависимыми вариантами.
3. Для сравнения групп с попарно-независимыми вариантами (хотя бы одна из них должна быть большой), воспользуйтесь формулой, представленной на рисунке. С помощью формулы вы сможете найти критерий Стьюдента, именно по нему определяют доверительную вероятность различия двух групп.
   
4. Чтобы определить критерий Стьюдента для групп небольшого размера с попарно-независимыми вариантами, применяйте другую формулу, она представлена на втором рисунке. Число степеней свободы рассчитывается так же, как и в первом случае: сложите объемы двух выборок и вычтите число 2.
   
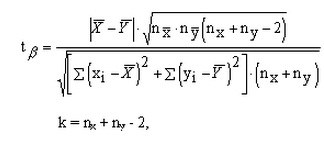
5. Сравнить две малые группы с попарно-зависимыми результатами можно при помощи двух формул, на ваш выбор. При этом число степеней свободы рассчитывается иначе, по формуле k=2*(n-1).
   
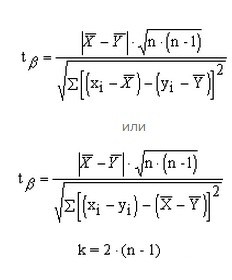
6. Далее определите доверительную вероятность по таблице t-критериев Стьюдента. При этом учтите, чтобы выборка была достоверной, доверительная вероятность должна быть не менее 95%. То есть найдите в первом столбце свое значение числа степеней свободы, а в первой строке – рассчитанный критерий Стьюдента и оцените, меньше или больше полученная вероятность 95%.
7. Например, вы получили t=2,3; k=73. По таблице определите доверительную вероятность, она больше 95%, следовательно, различия выборок достоверны. Другой пример: t=1,4; k=70. По таблице, чтобы получить минимальное значение достоверности 95%, для k=70, t должно быть равно хотя бы 1,98. У вас же оно меньше - всего 1,4, поэтому различие выборок недостоверно.