Вам понадобится
- - лист бумаги;
- - линейка;
- - карандаш.
Инструкция
1
Постройте чертеж фигуры, вращением которой будет образовываться искомое тело. Чертеж должен быть выполнен в координатной сетке X0Y, а фигура - ограничиваться строго определенными линиями функций. Не забывайте, что даже простейшие фигуры, например, квадрат, ограничиваются линиями функций. Для простоты вычислений ось вращения задайте линией Y=0.
2
По представленной формуле вычислите объем тела вращения. При этом не забывайте значение числа Пи, равное 3,1415926. Пределами интегрирования a и b возьмите точки пересечения функции с осью 0Y. Если в практическом задании плоская фигура расположена ниже оси 0Y, функцию в формуле возведите в квадрат. При вычислении интеграла будьте внимательны, чтобы не допустить ошибки.
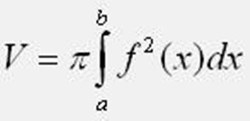
3
В ответе обязательно указывайте, что объем вычислен в кубических единицах, если условия задачи не определяют конкретных единиц измерения.
4
Если в задании необходимо вычислить объем тела, образованного вращением фигуры сложной формы, попробуйте упростить его. Например, разбейте плоскую фигуру на несколько более простых, затем вычислите объемы тел вращения и сложите результаты. Или наоборот, дополните плоскую фигуру до более простой, а объем искомого тела вращения вычислите как разность объемов тел.
5
Если плоская фигура образована синусоидами, пределами интегрирования в большинстве случаев будут 0 и Пи/2. Также будьте внимательны при построении графиков тригонометрических функций. Если аргумент будет делиться на два X/2, графики растягивайте по оси 0X в два раза. Для самопроверки точности чертежа найдите 3-4 точки по тригонометрическим таблицам.
6
Аналогичным образом вычислите объем тела, образованного вращением плоской фигуры вокруг оси 0X. Для этого перейдите к обратным функциям и проведите интегрирование по вышеприведенной формуле. Переход к обратной функции, другими словами - это выражение X через Y. Обратите внимание: пределы интегрирования расставляйте строго снизу вверх по оси ординат.
Видео по теме