Инструкция
1
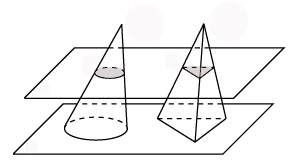
Для начала вспомним принцип Кавальери. Этот принцип утверждает, что если две объемные фигуры можно расположить таким образом, чтобы при сечении их параллельными плоскостями получались плоские фигуры одинаковой площади, то эти трехмерные фигуры равного объема.
2
Рассмотрим пирамиду той же высоты и площади основания, что и конус. Рассечем конус и эту пирамиду одной плоскостью. В сечении конуса будет круг, в сечении пирамиды - треугольник. При этом в сечении их по основанию получим плоские фигуры равной площади. Тогда для данных объемных фигур работает принцип Кавальери, а значит конус имеет тот же объем, что и пирамида.
3
Для треугольной пирамиды справедлива следующая формула вычисления объема: V = S*h/3, где S - площадь основания, а h - высота пирамиды.
4
Тогда для конуса также справедлива формула: V = S*h/3. При этом площадь основания конуса легко выразить через радиус: S = πR². Тогда объем конуса: V = S = πR²h/3.
Видео по теме
Обратите внимание
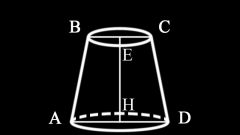
Для конуса, усеченного плоскостью, параллельной основанию, справедлива следующая формула расчета объема: V = πh (R²+Rr+r²), где r - радиус окружности сечения.
Источники:
- Длина образующей конуса равна l, а длина окружности основания