Инструкция
1
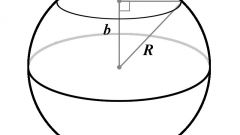
Используйте классическую формулу объема (V) сферы, если из условий известен ее радиус (r) - возведите радиус в третью степень, умножьте на число Пи, а результат увеличьте еще на треть. Записать эту формулу можно так: V=4*π*r³/3.
2
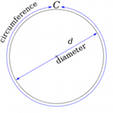
Если есть возможность измерить диаметр (d) сферы, то поделите его пополам и используйте как радиус в формуле из предыдущего шага. Или найдите одну шестую часть от возведенного в куб диаметра, умноженного на число Пи: V=π*d³/6.
3
Если известен объем (v) цилиндра, в который вписана сфера, то для нахождения ее объема определите, чему равны две трети от известного объема цилиндра: V=⅔*v.
4
5
Воспользуйтесь какими-либо мерными емкостями в качестве подручных средств для измерения объема сосуда сферической формы. Например, наполните его водой, измеряя с помощью мерной емкости количество заливаемой жидкости. Полученное значение в литрах переведите в кубические метры - эта единица принята в международной системе СИ для измерения объема. В качестве коэффициента перевода из литров в кубометры используйте число 1000, так как один литр приравнен к одному кубическому дециметру, а их в каждый кубический метр вмещается ровно тысяча штук.
6
Используйте принцип измерения, противоположный описанному в предыдущем шаге, если тело в форме сферы нельзя наполнить жидкостью, но можно погрузить в нее. Заполните мерный сосуд водой, отметьте уровень, погрузите измеряемое сферическое тело в жидкость и по разнице уровней определите количество вытесненной воды. Затем переведите полученный результат из литров в кубометры так же, как это описано в предыдущем шаге.
Видео по теме
Источники:
- объем полусферы