Вам понадобится
- - бумага;
- - ручка.
Инструкция
1
Определение: Корреляционным моментом ССВ X и Y называется смешанный центральный момент второго порядка (см. рис.1)
Здесь W(x,y) – совместная плотность вероятности ССВ
Корреляционный момент является характеристикой: а) взаимного разброса значений ССВ относительно точки средних значений или математических ожиданий (mx, my); б) степени линейной связи между СВ Х и Y.
Здесь W(x,y) – совместная плотность вероятности ССВ
Корреляционный момент является характеристикой: а) взаимного разброса значений ССВ относительно точки средних значений или математических ожиданий (mx, my); б) степени линейной связи между СВ Х и Y.
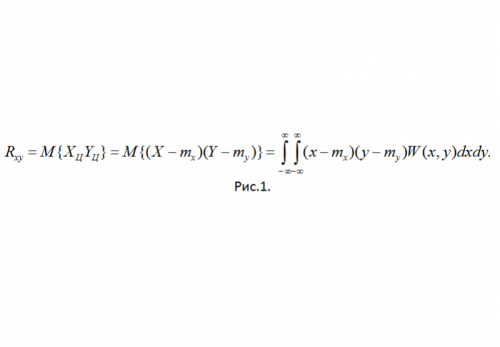
2
Свойства корреляционного момента.
1. R(xy)=R(yx) – из определения.
2. Rxx=Dx (дисперсии) - из определения.
3. Для независимых Х и Y R(xy)=0.
Действительно, при этом M{Xц,Yц}=M{Xц}M{Yц}=0. В данном случае это отсутствие линейной связи, но не любой, а, скажем, квадратичной.
4. При наличии «жесткой линейной связи между X и Y, Y=aX+b – |R(xy)|=бxбy=max.
5. –бxбy≤R(xy)≤бxбy.
1. R(xy)=R(yx) – из определения.
2. Rxx=Dx (дисперсии) - из определения.
3. Для независимых Х и Y R(xy)=0.
Действительно, при этом M{Xц,Yц}=M{Xц}M{Yц}=0. В данном случае это отсутствие линейной связи, но не любой, а, скажем, квадратичной.
4. При наличии «жесткой линейной связи между X и Y, Y=aX+b – |R(xy)|=бxбy=max.
5. –бxбy≤R(xy)≤бxбy.
3
Теперь вернемся к рассмотрению коэффициента корреляции r(xy), смысл которого заключается в линейной связи между СВ. Его значение изменяется от -1 до 1, кроме того он не обладает размерностью. В соответствии со сказанным, можно записать:
R(xy)= R(xy)/бxбy (1)
R(xy)= R(xy)/бxбy (1)
4
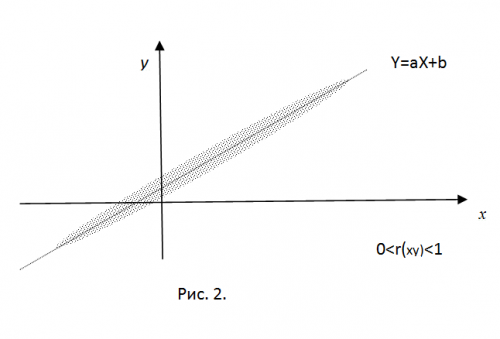
Для пояснения смысла нормированного корреляционного момента, представьте себе, что полученные опытным путем значения СВ Х и Y являются координатами точки на плоскости. При наличии «жесткой» линейной связи эти точки в точности лягут на прямую линию Y=aX+b. Возьмтие только положительные значения корреляции (при а
5
При r(xy)=0 все полученные точки окажутся внутри эллипса с центром в (mx, my), величина полуосей которого определяется значениями дисперсий СВ.
На этом вопрос о расчете r(xy), казалось бы, можно считать исчерпанным (см. формулу (1)). Проблема заключается в том, что исследователь, получивший значения СВ экспериментально, не может на все 100% знать плотность вероятности W(x,y). Поэтому лучше считать, что в поставленной задаче рассматриваются выборочные значения СВ (то есть полученными в опыте), и использовать оценки нужных величин. Тогда оценка
mx*=(1/n)(x1+x2+…+xn) (для СВ Y аналогично). Dx*=(1/(n-1))((x1- mx*)^2+ (x2- mx*)^2+…
+(xn- mx*)^2). R*x=(1/(n-1))((x1- mx*)(y1- my*)+(x2- mx*)(y2- my*)+…+(xn- mx*)(yn- my*)). бx*=sqrtDx (то же для СВ Y).
Теперь можно смело для оценок использовать формулу (1).
На этом вопрос о расчете r(xy), казалось бы, можно считать исчерпанным (см. формулу (1)). Проблема заключается в том, что исследователь, получивший значения СВ экспериментально, не может на все 100% знать плотность вероятности W(x,y). Поэтому лучше считать, что в поставленной задаче рассматриваются выборочные значения СВ (то есть полученными в опыте), и использовать оценки нужных величин. Тогда оценка
mx*=(1/n)(x1+x2+…+xn) (для СВ Y аналогично). Dx*=(1/(n-1))((x1- mx*)^2+ (x2- mx*)^2+…
+(xn- mx*)^2). R*x=(1/(n-1))((x1- mx*)(y1- my*)+(x2- mx*)(y2- my*)+…+(xn- mx*)(yn- my*)). бx*=sqrtDx (то же для СВ Y).
Теперь можно смело для оценок использовать формулу (1).
Источники:
- Свойства коэффициента корреляции