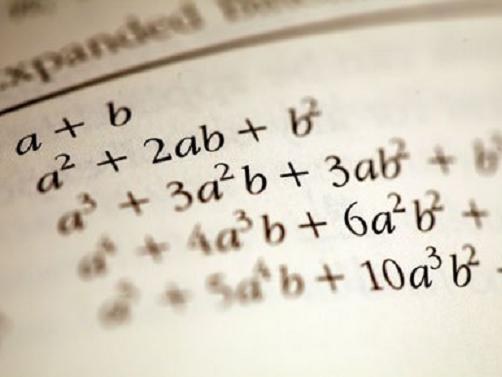Инструкция
1
2
Многочлены применяются во многих разделах, в том числе рассмотрении нуля, отрицательных и комплексных чисел, теории групп, колец, узлов, множеств и т.д. Использование полиномиальных вычислений значительно упрощает выражение свойств разных объектов.
3
Основные определения многочлена:
• Каждое слагаемое полинома называется одночленом или мономом.
• Многочлен, состоящий из двух одночленов, называют двучленом или биномом.
• Коэффициенты полинома – вещественные или комплексные числа.
• Если старший коэффициент равен 1, то многочлен называют унитарным (приведенным).
• Степени переменной в каждом одночлене – целые неотрицательные числа, максимальная степень определяет степень многочлена, а его полной степенью называется целое число, равное сумме всех степеней.
• Одночлен, соответствующий нулевой степени, называется свободным членом.
• Многочлен, все одночлены которого имеют одинаковую полную степень, называется однородным.
• Каждое слагаемое полинома называется одночленом или мономом.
• Многочлен, состоящий из двух одночленов, называют двучленом или биномом.
• Коэффициенты полинома – вещественные или комплексные числа.
• Если старший коэффициент равен 1, то многочлен называют унитарным (приведенным).
• Степени переменной в каждом одночлене – целые неотрицательные числа, максимальная степень определяет степень многочлена, а его полной степенью называется целое число, равное сумме всех степеней.
• Одночлен, соответствующий нулевой степени, называется свободным членом.
• Многочлен, все одночлены которого имеют одинаковую полную степень, называется однородным.
4
Некоторые часто используемые многочлены названы по фамилии ученого, который их определил, а также описал функции, которые они задают. Например, Бином Ньютона – это формула для разложения полинома двух переменных на отдельные слагаемые для вычисления степеней. Это известные из школьной программы записи квадратов суммы и разности (a + b)^2 – a^2 + 2*a*b + b^2, (a – b)^2 = a^2 – 2*a*b + b^2 и разность квадратов (a^2 – b^2) = (a - b)*(a + b).
5
Если допустить в записи многочлена отрицательные степени, то получится многочлен или ряд Лорана; многочлен Чебышева используется в теории приближений; многочлен Эрмита – в теории вероятностей; Лагранжа – для численного интегрирования и интерполяции; Тейлора – при аппроксимации функции и т.д.
Обратите внимание
Бином Ньютона часто упоминают в книгах («Мастер и Маргарита») и фильмах («Сталкер»), когда герои решают математические задачи. Этот термин на слуху, поэтому считается самым известным многочленом.