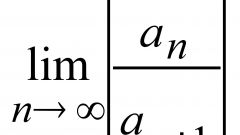Вам понадобится
  • Умение вычислять пределы последовательностей.
Инструкция
1
Определите формулу общего члена ряда. Пусть дан ряд x1+x2+…+xn+…, его общий член имеет вид xn. Воспользуйтесь признаком Коши определения сходимости ряда. Посчитайте предел lim((xn)^(1/n)) при n стремящимся к ∞. Пусть он существует и равен L, тогда если L<1, то ряд сходится, если L>1, то ряд расходится, а если L=1, то необходимо дополнительно исследовать ряд на сходимость.
2
Рассмотрите примеры. Пусть дан ряд 1/2+1/4+1/8+…, общий член ряда представляется в виде 1/(2^n). Найдите предел lim((1/(2^n)^(1/n)) при n стремящимся к ∞. Этот предел равен 1/2<1 и, следовательно, ряд 1/2+1/4+1/8+… сходится. Или, например, пусть имеется ряд 1+16/9+216/64+…. Представьте общий член ряда в виде формулы (2×n/(n+1))^n. Посчитайте предел lim(((2×n/(n+1))^n)^(1/n))=lim(2×n/(n+1)) при n стремящимся к ∞. Предел равен 2>1, то есть данный ряд расходится.
3
Определите сходимость ряда по признаку Даламбера. Для этого посчитайте предел lim((xn+1)/xn) при n стремящимся к ∞. Если этот предел существует и равен M<1, то ряд сходится, если M>1, то ряд расходится. Если M=1, то ряд может быть сходящимся и расходящимся.
4
Изучите несколько примеров. Пусть дан ряд Σ(2^n/n!). Посчитайте предел lim((2^(n+1)/(n+1)!)×(n!/2^n))=lim(2/(n+1)) при n стремящимся к ∞. Он равен 0<1 и данный ряд является сходящимся. Пусть теперь дан ряд Σn!×(6/n)^n. Вычислите предел lim((n+1)!×6^(n+1)×n^n)/((n+1)^(n+1)×n!×6^n)=lim (6/(1+1/n)^n)=6/e>1 и значит данный ряд расходится.
5
Воспользуйтесь признаком Лейбница для знакочередующегося ряда при условии, что xn>x(n+1). Посчитайте предел lim(xn) при n стремящимся к ∞. Если этот предел равен 0, то ряд сходится, его сумма положительна и не превосходит первого члена ряда. Например, пусть дан ряд 1−1/2+1/3−1/4+…. Заметьте, что 1>1/2>1/3>…>1/n>…. Общий член ряда будет 1/n. Посчитайте предел lim(1/n) при n стремящимся к ∞. Он равен 0 и, следовательно, ряд сходится.