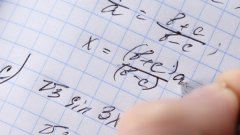Инструкция
1
Степенной ряд – это частный случай функционального ряда. Он имеет вид 0+c1(z-z0)+c2(z-z0)^2+…+cn(z-z0)^n+… . (1)Если сделать подстановку x=z-z0, то этот ряд примет вид c0+c1x+c2x^2+…+cn(x^n)+… . (2)
2
В данном случае ряды вида (2) более удобны для рассмотрения. Очевидно, что любой степенной ряд сходится при х=0. Множество точек, в которых ряд является сходящимся (область сходимости), можно найти опираясь на теорему Абеля. Из нее следует, что если ряд (2) является сходящимся в точке x0≠0, то он сходится для всех х, удовлетворяющих неравенству |x|
3
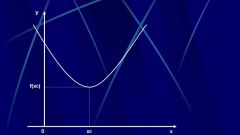
Соответственно, если в некоторой точке х1 ряд расходится, то это наблюдается при всех х, для которых |x1|>|b|. Иллюстрация рис.1, где х1 и х0 выбраны большими нуля, позволяет понять, что все х1>x0. Поэтому при их сближении неминуемо возникнет ситуация х0=х1. В этом случае ситуация со сходимостью, при прохождении слившихся точек (назовем их –R и R) меняется скачкообразно. Поскольку геометрически R длина, то число R≥0 называется радиусом сходимости степенного ряда (2). Интервал (-R,R) называется интервалом сходимости степенного ряда. Возможно и R=+∞. При x=±R ряд становится числовым и его анализ производится на основе сведений о числовых рядах.
4
Для определения R ряд исследуется на абсолютную сходимость. То есть составляется ряд из абсолютных величин членов исходного ряда. Исследования можно проводить на основе признаков Даламбера и Коши. При их применении отыскиваются пределы, которые сравниваются с единицей. Поэтому предел равный единице достигается при х=R. При решении по признаку Даламбера сначала отыскивается предел, представленный на рис. 2а. Положительное число х, при котором этот предел равен единице, будет являться радиусом R (см. рис. 2b). При исследовании ряда по радикальному признаку Коши формула для вычисления R примет вид (см. рис. 2c).
5
Формулы, представленные на рис. 2 применяются при условии, что рассматриваемые пределы существуют. Для степенного ряда (1) интервал сходимости записывается в виде (z0-R, z0+R).