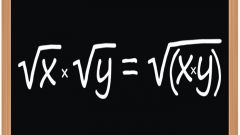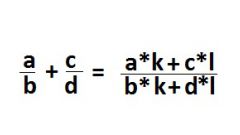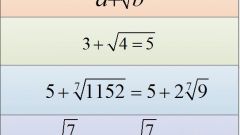Как сравнивать корни

Корнем n-ой степени из действительного числа a называется такое число b, для которого выполняется равенство b^n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени - только для положительных. Значением корня часто является бесконечная десятичная дробь, что затрудняет его точное вычисление, поэтому важно уметь сравнивать корни.

Инструкция

1. Пусть требуется сравнить два иррациональных числа. Первое, на что следует обратить внимание - это показатели степени корней у сравниваемых чисел. Если показатели одинаковы, то сравнивают подкоренные выражения. Очевидно, что чем больше подкоренное число, тем больше значение корня при равных показателях. Например, пусть надо сравнить кубический корень из двух и кубический корень из восьми. Показатели одинаковы и равны 3, подкоренные выражения 2 и 8, причем 2 < 8. Следовательно, и кубический корень из двух меньше кубического корня из восьми.
2. В другом случае показатели степени могут быть разными, а подкоренные выражения одинаковыми. Тоже вполне понятно, что при извлечении корня большей степени получится меньшее число.Возьмите для примера кубический корень из восьми и корень шестой степени из восьми. Если обозначить значение первого корня как a, а второго - как b, то a^3 = 8 и b^6 = 8. Легко видеть, что a должно быть больше b, таким образом кубический корень из восьми больше корня шестой степени из восьми.
3. Более сложной представляется ситуация с разными показателями степени корня и разными подкоренными выражениями. В таком случае надо найти наименьшее общее кратное для показателей корней и возвести оба выражения в степень, равную наименьшему общему кратному.Пример: надо сравнить 3^1/3 и 2^1/2 (математическая запись корней есть на рисунке). Наименьшее общее кратное для 2 и 3 равно 6. Возведите оба корня в шестую степень. Тут же получится, что 3^2 = 9 и 2^3 = 8, 9 > 8. Следовательно, и 3^1/3 > 2^1/2.