Как сложить модуль

Модулем числа x или её абсолютной величиной называется конструкция вида |x|. В обобщённом смысле модуль – это норма элемента многомерного векторного пространства и обозначается как ||x||. Модуль числа не может быть отрицательным, для одного и того же числа взятого с противоположными знаками, модуль будет одинаковым.

Инструкция

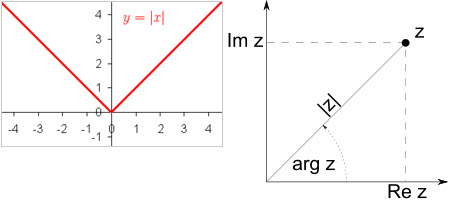
1. Модуль вещественного или комплексного числа – это расстояние от начала координат до заданной точки, именно поэтому он не может быть отрицательным. Модуль определён на промежутке (-?;+?), а принимаемые значения лежат в интервале [0;+?).
   
2. Модуль действительного числа является непрерывной кусочно - линейной функцией и раскрывается по формуле представленной на рисунке. Эту формулу необходимо учитывать при выполнении операций над модулями.
   
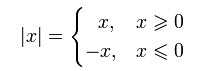
3. Над абсолютными величинами можно производить арифметические операции, при этом необходимо учитывать свойства модулей.
   Сумма модулей чисел x и y больше или равна модулю суммы этих чисел, т.е.
   |x| + |y| ? |x + y|, это соотношение называется неравенством треугольника.
   Модуль суммы чисел x и y больше или равен разности модулей этих чисел, т.е.
   |x + y| ? |x| - |y|.
   Сумма модулей чисел x и y больше или равна модулю разности этих чисел, т.е.
   |x| + |y| ? |x - y|.
   Кроме того справедливо следующее соотношение
   |x ± y| ? ||x| - |y||.