Модуль представляет собой абсолютную величину выражения. Для обозначения модуля применяют прямые скобки. Заключенные в них значения считаются взятыми по модулю. Решение модуля состоит в раскрытии модульных скобок по определенным правилам и нахождении множества значений выражения. В большинстве случаев модуль раскрывается таким образом, что подмодульное выражение получает ряд положительных и отрицательных значений с том числе и нулевое значение. Исходя из данных свойств модуля, составляются и решаются далее уравнения и неравенства исходного выражения.
Запишите исходное уравнение с модулем. Для его решения раскройте модуль. Рассмотрите каждое подмодульное выражение. Определите, при каком значении входящих в него неизвестных величин выражение в модульных скобках обращается в ноль.
2
Для этого приравняйте подмодульное выражение к нулю и найдите решение получившегося уравнения. Запишите найденные значения. Таким же образом определите значения неизвестной переменной для каждого модуля в заданном уравнении.
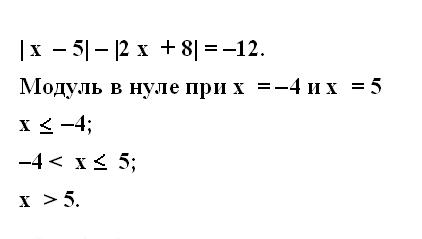
3
Рассмотрите случаисуществования переменных, когда они отличны от нуля. Для этого запишите систему неравенств для всех модулей исходного уравнения. Неравенства должны охватывать все возможные значения переменной на числовой прямой.
4
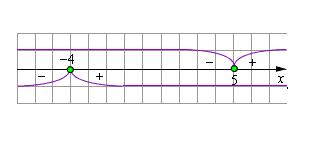
Нарисуйте числовую прямую и отложите на ней полученные значения. Значения переменной в нулевом модуле будут служить ограничениями при решении модульного уравнения.
5
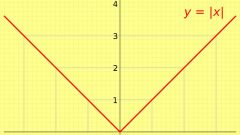
В исходном уравнении нужно раскрыть модульные скобки, меняя знак выражения так, чтобы значения переменной соответствовали отображенным на числовой прямой. Решите полученное уравнение. Найденное значение переменной проверьте на ограничение, заданное модулем. Если решение удовлетворяет условию, значит оно истинно. Не удовлетворяющие ограничениям корни должны отбрасываться.
6
Аналогичным образом раскрывайте модули исходного выражения с учетом знака и высчитывайте корни получаемого уравнения. Запишите все полученные корни, удовлетворяющие неравенствам ограничения.
