Инструкция
1
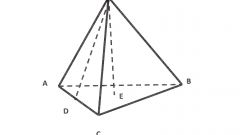
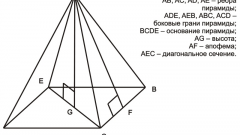
Для правильной треугольной пирамиды верна общая для таких многогранников формула определения объема (V) пространства, заключенного внутри граней фигуры. Она связывает этот параметр с высотой (H) и площадью основания (s). Так как в нашем случае все грани одинаковы, не обязательно знать площадь именно основания - для вычисления объема перемножьте площадь любой грани на высоту, а результат поделите на три части: V = s*H/3.
2
Если известна полная площадь поверхности (S) пирамиды и ее высота (H), для определения объема (V) используйте формулу предыдущего шага, увеличив в четыре раза знаменатель: V = S*H/12. Это вытекает из того, что общая площадь фигуры складывается именно из четырех одинаковых по размерам граней.
3
Площадь правильного треугольника равна четверти произведения квадрата длины ее стороны на корень из тройки. Поэтому для нахождения объема (V) по известной длине ребра (a) правильного тетраэдра и его высоте (H) используйте такую формулу: V = a²*H/(4*√3).
4
Впрочем, зная длину ребра (a) правильной треугольной пирамиды, можно рассчитать ее объем (V) без использования высоты или каких-либо других параметров фигуры. Возведите единственную необходимую величину в куб, умножьте на квадратный корень из двойки и поделите результат на двенадцать: V = a³*√2/12.
5
Верно и обратное - знания высоты тетраэдра (H) достаточно для вычисления объема (V). Длину ребра в формуле предыдущего шага можно заменить утроенной высотой, поделенной на квадратный корень из шестерки: V = (3*H/√6)³*√2/12 = 27*√2*H³/(12*(√6)³). Чтобы избавиться от всех этих корней и степеней замените их десятичной дробью 0,21651: V = H³*0,21651.
6
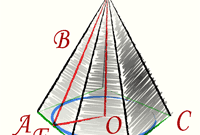
Если правильная треугольная пирамида вписана в сферу известного радиуса (R), формула вычисления объема (V) может быть записана так: V = 16*√2*R³/(3*(√6)³). Для практических расчетов замените все степенные выражения одной десятичной дробью достаточной точности: V = 0,51320*R³.