Как найти моду по статистике

Статистика – это функция результатов наблюдений, с помощью которой можно найти оценку неизвестного параметра распределения. Для такой характеристики статистического распределения, как мода, оценка не вычисляется, а выбирается поcле первичной статистической обработки имеющейся выборки. Лишь в отдельных случаях и только после получения теоретического распределения моду можно найти через другие числовые характеристики.

Инструкция

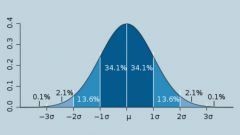
1. Согласно литературным данным, мода дискретной случайной величины (обозначение Мо) – это наиболее вероятное ее значение. Такое определение не подходит к непрерывным распределениям, для них это такое значение случайной величины Х=Мо, при котором достигается максимум плотности вероятности W(x). W(Mo)=max. Поэтому для теоретических распределений следует взять производную от плотности вероятности, решить уравнение W’(x)=0 и положить равным моде его корень. Некоторые распределения не имеют моды (антимодальные). Известное равномерное распределение является безмодальным. Встречаются и многомодальные случаи. Мо относится к характеристикам положения случайной величины.
2. Для статистических распределений мода выбирается практически так же. Прежде всего, проведите обработку имеющейся выборки методами математической статистики. Если имелась выборка значений заведомо дискретной случайной величины, то примите равным оценке моды Мо* значение, которое встречалось чаще других. Полигон при этом строить не обязательно.
3. При обработке опытных данных, полученных в результате наблюдений непрерывной случайной величины, всю выборку разбивают на отдельные разряды и вычисляют частоты этих разрядов, как pi*=ni/n. Здесь ni – число наблюдений, приходящихся на i-й разряд, а n – объем выборки. В первом приближении pi* можно считать вероятностями дискретных значений случайной величины. Для самих значений используйте числа, соответствующие серединам разрядов. В качестве Мо* возьмите то число, которому соответствует наибольшая частота.
4. Оценка моды может быть использована, например, в радиосвязи, для разработки приемников, оптимальных по критерию максимума апостериорной плотности вероятности. Выбор Мо*, как середины наиболее вероятного разряда, строго говоря, не обязателен. Просто в пределах каждого из разрядов распределение считается равномерным. Поэтому в данном случае Мо* скорее интервальная, а не точечная оценка, и с одинаковой вероятностью может равняться любому числу из выбранного разряда.