Как найти сигму

«Сигмой», буквой греческого алфавита σ, принято называть постоянную величину среднеквадратичной ошибки случайных погрешностей измерений. Вычисление сигмы широко используется в физике, статистике и близких к ним сферах деятельности человека. Далее представлен алгоритм расчета сигмы.

Вам понадобится

• • Массив данных для вычисления сигмы;
• • Формулы для расчета;
• • Калькулятор или компьютер с установленным на нем ПО Microsoft Excel.

Инструкция

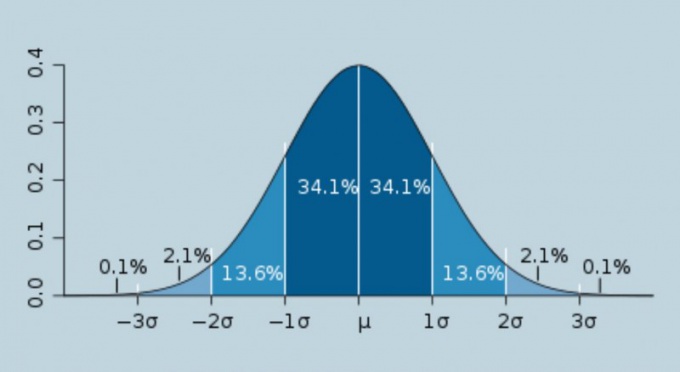
1. Стандартную или среднюю квадратичную погрешность измерений называют также стандартом измерений. Эта величина вычисляется по формуле, изображенной на картинке.
2. Следует учесть, что величиной, которую принято называть сигмой, является постоянное значение, к которому стремится значение среднеквадратичной погрешности Sn при бесконечно большом количестве измерений. Чем больше будет число измерений, тем ближе будет оно к сигме. Данное выражение можно представить в виде, изображенном на картинке.
3. Вычислите сигму на практике. Выпишите значения всех измерений в один столбец. Вычислите среднее арифметическое для всех значений, суммируя их вместе и поделив на количество значений.
4. Из среднего арифметического вычтите каждое i-ое значение и возведите его в квадрат. Просуммируйте все полученные значения и разделите результат на n-1 (количество значений минус один).
5. Полученное значение в статистике принято называть дисперсией. Извлекаем из него квадратный корень. В результате получаем стандартную среднеквадратичную погрешность, именуемую сигмой.
6. Данные вычисления можно производить в стандартном пакете для работ с электронными таблицами Microsoft Excel. Их можно сделать как пошагово по описанной выше методике, так и простым назначением функции СТАНДОТКЛОН. Проверьте заранее, что ячейка со значениями имеет числовой формат. Обязательно укажите диапазон значений для вычисления сигмы.