Инструкция
1
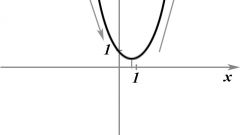
Найдите производную функции. Например, для функции y = 2x/(x*x + 1) производная будет вычисляться следующим образом:y’ = (2 (x*x + 1) – 2x*2x ) / (x*x + 1) * (x*x + 1) = (2 – 2x*x) / (x*x + 1) * (x*x + 1).
2
Приравняйте найденную производную к нулю:(2 – 2x*x) / (x*x + 1) * (x*x + 1) = 0;2- 2x*x = 0;(1 – x)(1 + x) = 0.
3
Определите значение переменной полученного выражения, то есть то значение, при котором переменная становится равной нулю. Для рассматриваемого примера получим:x1 = 1, x2 = -1.
4
Используя полученные на предыдущем шаге значения, разбейте координатную прямую на промежутки. Нанесите на прямую также точки разрыва функции. Совокупность таких точек на оси координат называется точками, «подозрительными» на экстремум. В нашем примере прямая будет разбита на три промежутка: от минус бесконечности до -1; от -1 до 1; от 1 до плюс бесконечности.
5
Вычислите, на каких из получившихся промежутков производная функции будет положительной, а на каких она примет отрицательное значение. Для этого подставьте значение из промежутка в производную.
6
Для первого промежутка возьмите, например, значение -2. При этом производная будет равняться -0,24. Для второго промежутка возьмите значение 0; производная функции составит -0,24. Взятое на третьем промежутке значение, равное 2, даст производную -0,24.
7
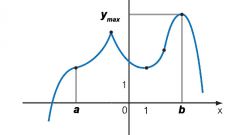
Рассмотрите последовательно все промежутки между точками, соединяющими отрезки. Если при прохождении через «подозрительную» точку производная меняет знак с плюса на минус, то такая точка будет максимумом функции. Если имеет место смена знака с минуса на плюс, перед нами точка минимума.
8
Как мы видим из примера, проходя через точку -1, производная функции меняет знак с минуса на плюс. Иными словами, это и есть точка минимума. При прохождении через 1 знак меняется с плюса на минус, поэтому мы имеем дело с экстремумом, называемым точкой максимума функции.
9
Вычислите значение рассматриваемой функции на концах отрезка и найденных точках экстремума. Выберите наименьшее и наибольшее значения.