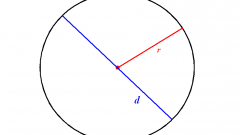
Пи («π») представляет из себя математическую константу, полученную довольно интересным путем. Допустим, что диаметр окружность равен 1 условной единице. Тогда число π — это длина данной окружности, которая приблизительно равна 3,14 условных единиц. Говоря другими словами, число «пи» выражает соотношение между длиной окружности и ее диаметром. Это соотношение будет всегда постоянным.
Пи обладает рядом свойств.
Во-первых, число π иррационально, это означает, что его нельзя представить в виде правильной дроби. Значение 3,14 является достаточно приблизительным, доподлинно не известно, сколько же знаков после запятой у этой константы.
Во-вторых, число π — трансцендентное. Это означает, что оно никогда не может быть степенью какого-либо корня из другого числа. Говоря иначе, число π не является алгебраическим. Более того, если какое-либо число возвести в степень π, то опять же получится трансцендентное число.
Стоит отметить, что древние математики Египта, Греции, Рима, Сирии и Ирана уже знали, что соотношение между диаметром окружности и ее длиной является постоянной величиной. К примеру, в Вавилоне это соотношение оценивалось как 25/8, а в Египте как 256/81. Но наибольших успехов в вычислении значения числа π добился Архимед, который путем многократного описывания вокруг окружности и вписывания в нее правильных многоугольников добился довольно точных результатов. Периметр вписанного многоугольника Архимед принял за минимальное значение числа π, а описанного — за максимальное. Таким образом, Архимед вывел значение константы π, равное 3.142857142857143.
Забавно отметить, что существует праздник «День числа π», который празднуется 14 марта. Это происходит потому, что если записать числами день и дату праздника, то получится 3.14 — приблизительное значение данной константы. По другой версии, этот праздник надо отмечать 22 июля, так как 22/7 тоже является одним из первых соотношений, приблизительно равным 3.14