Как составить магический квадрат

Математические головоломки иногда увлекают так, что хочется научиться создавать их, а не только решать. Пожалуй, самым интересным для новичков является создание магического квадрата, который представляет собой квадрат с размерами сторон nxn, в который вписаны натуральные числа от 1 до n2 так, что сумма чисел по горизонталям, вертикалям и диагоналям квадрата является одинаковой и равняется одному числу.

Инструкция

1. Прежде чем составлять свой квадрат, усвойте, что магических квадратов второго порядка не бывает. Магический квадрат третьего порядка существует фактически только один, остальные производные от него получаются с помощью поворота либо отражения основного квадрата по оси симметрии. Чем больше порядок, тем больше существует возможных волшебных квадратов этого порядка.
2. Изучите основы построения. Правила построения разных магических квадратов подразделяются на три группы по порядку квадрата, а именно он может быть нечетным, равным удвоенному или учетверенному нечетному числу. Общей методики для построения всех квадратов в настоящее время не существует, хотя широко распространены разные схемы.
3. Воспользуйтесь компьютерной программой. Скачайте нужное приложение и введите желаемые значения квадрата (2-3), программа сама генерирует нужные цифровые комбинации.
4. Постройте квадрат самостоятельно. Возьмите матрицу n x n , внутри которой произведите построение ступенчатого ромба. В нем заполните все квадратики слева и вверх по всем диагоналям последовательностью нечетных чисел.
5. Определите значение центральной ячейки О. В углах магического квадрата расположите такие числа: верхняя правая ячейка - О-1, нижняя левая - О+1, правая внизу - О-n, а левая вверху - О+n. Пустые ячейки в угловых треугольниках заполните, используя достаточно простые правила: в строках по направлению слева направо числа увеличиваются на n + 1, а в столбиках по направлению сверху вниз числа увеличиваются на n-1.
6. Обнаружить все квадраты с порядком равным n удается только для n\le 4, поэтому интересны отдельные процедуры для построения магических квадратов с n > 4. Проще всего рассчитать конструирование такого квадрата нечетного порядка. Воспользуйтесь специальной формулой, куда требуется просто поставить необходимые данные для получения желаемого результата.
   
   Например, константа квадрата, построенного по схеме с рис. 1, вычисляется по формуле:
   
   S = 6a1 +105b,
   где a1 – первый член прогрессии,
   b – разность прогрессии.
   
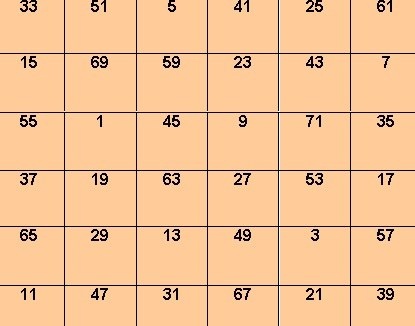
7. Для квадрата, изображенного на рис. 2, формула:
   
   S = 6*1 + 105*2 = 216
   
8. Кроме этого, существуют алгоритмы для построения пандиагональных квадратов и идеальных магических квадратов. Воспользуйтесь специальными программами построения этих моделей.