Вам понадобится
- циркуль, линейка, карандаш
Инструкция
1
Для решения задачи необходимо сделать несколько оговорок, так как не каждый треугольник возможно вписать в заданный квадрат. Во-первых, считаем, что квадрат имеет сторону равную а. Во-вторых, треугольник также имеет определенные величины своих сторон: АВ, ВС, АС. Длина наибольшей из сторон треугольника (по крайне мере остроугольного) АС больше или равна а, но не превышает длину диагонали квадрата EG, то есть |EG|≥|AC|≥a, где EG, согласно теореме Пифагора, равна а√2 . В случае рассмотрения задачи о вписывании тупоугольного треугольника в квадрат, одна из его сторон может накладываться на сторону заданного квадрата.
2
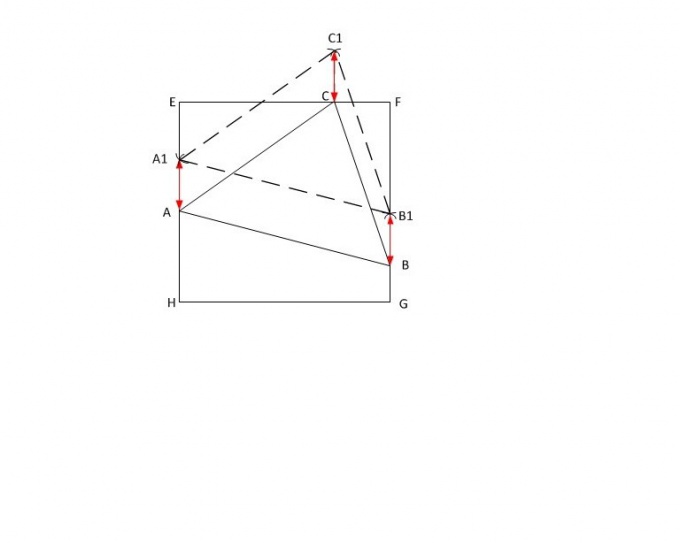
Пусть у треугольника АВС стороны имеют длины |АВ|, |ВС| и |АС|, соответственно, и |АС| наибольшая из них. В заданном квадрате EFGH продлите пунктиром две параллельные стороны (например EH и FG ) и поставьте произвольную точку А1 на стороне EH.
3
По линейке выставьте на циркуле длину |АС|. Установите его в точку А1 и начертите окружность. Точку пересечения нарисованной окружности со стороной квадрата FG обозначьте буквой Х. Перенесите туда циркуль и, не меняя радиуса, сделайте засечку на окружности за пределами квадрата. Отметьте ее буквой С1.
4
После этого из вершины А1 начертите окружность радиусом |АВ|, а из С1 – радиусом |ВС|. Точку их пересечения обозначьте С1. Из построенной точки опустите перпендикуляр на сторону квадрата EF, а точку их пересечения назовите С.
5
Замерьте линейкой длину h отрезка ВВ1. Отложите полученное значение от точек А1, С1 на соответствующие стороны квадрата и обозначьте концы отрезков буквами А и С. Теперь соедините вершины А,В и С заданного треугольника. Задача выполнена.
Видео по теме