Как доказать теорему Пифагора

Теорема Пифагора – это теорема геометрии, устанавливающая связь между сторонами прямоугольного треугольника. Теорема – это утверждение, для которого в рассматриваемой теории существует доказательство. На данный момент существует более 300 способов доказательства теоремы Пифагора, однако как базовый элемент школьной программы используется доказательство через подобные треугольники.

Вам понадобится

• страница тетради в клетку
• линейка
• карандаш

Инструкция

1. Теорема Пифагора звучит следующим образом: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Геометрическая формулировка требует ещё и понятия площади: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
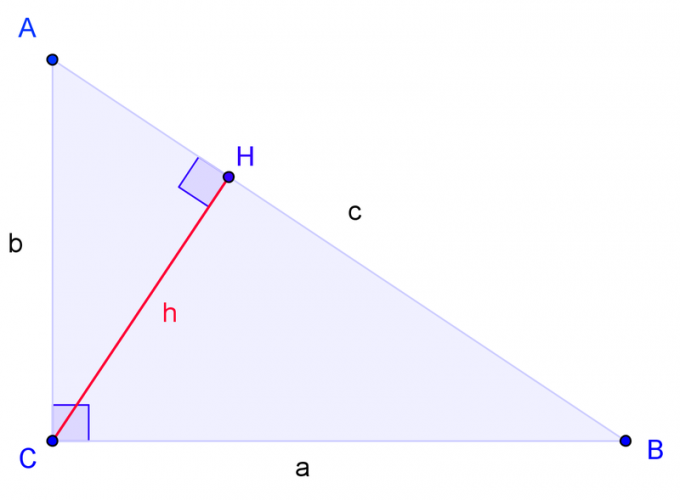
2. Начертите прямоугольный треугольник с вершинами A, B, C, где угол C – прямой. Сторону BC обозначьте a, сторону AC обозначьте b, сторону AB обозначьте c.
3. Проведите высоту из угла C и обозначьте её основание через H. Треугольники подобны, если два угла одного треугольника соответственно равны двум углам другого треугольника. Угол H – прямой, так же, как и угол C. Следовательно, треугольник ACH подобен треугольнику ABC по двум углам. Треугольник CBH также подобен треугольнику ABC по двум углам.
4. Составьте уравнение, где a относится к c, как HB относится к а. Соответственно, b относится к c, как AH относится к b.
5. Решите эти уравнения. Для того чтобы решить уравнение, помножьте числитель правой дроби на знаменатель левой дроби, а знаменатель правой дроби – на числитель левой дроби. Получаем: a в квадрате = сHB, b в квадрате = cAH.
6. Сложите эти два уравнения. Получаем: a в квадрате + b в квадрате = c (HB + AH). Так как HB + AH = c, то в результате должно получиться: a в квадрате + b в квадрате = c в квадрате. Что и требовалось доказать.