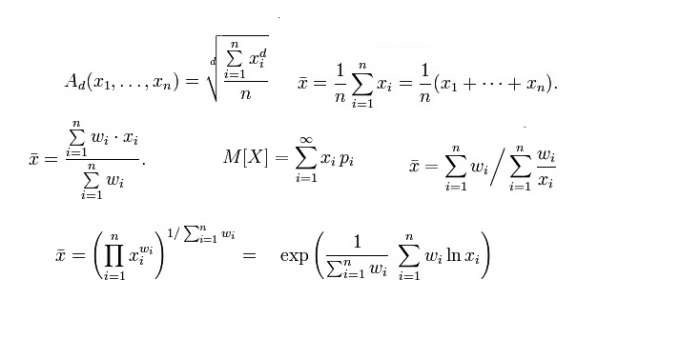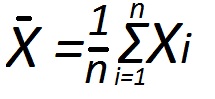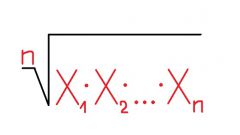Вам понадобится
- Учебники по высшей математике, теории вероятности, статистике
Инструкция
1
Итак, в математике наиболее распространен и востребован расчет среднего степенного значения функции по Колмогорову. Частными случаями Колмогоровских средних являются среднее арифметическое, среднее квадратичное, среднее гармоническое, среднее геометрическое. Для расчета среднего арифметического значения (или простого среднего), просуммируйте весь ряд чисел и поделите на их количество. Вычислите квадратный корень из среднего арифметического квадратов данных чисел, и вы получите среднее квадратичное значение. Среднее гармоническое и среднее геометрическое также несложно вычислить, путем подстановки ряда данных в формулы

2
Среднее взвешенное значение вычисляется, когда мы имеем дело с линейными комбинациями. Тут тоже существуют различные алгоритмы. Чаще всего используют среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное. Эти величины вы можете вычислить, воспользовавшись следующими формулами:

3
Хронологическое среднее используется для вычисления среднего значения абсолютных величин, меняющихся в определенном временном интервале. Для вычисления этого значения используйте данную формулу:

4
В статистике наиболее часто встречаются такие понятия как мода и медиана. Они являются непараметрическими средними. Напомним что мода - это наиболее часто встречающееся число в данном ряде, а медиана - некоторое значение признака, которое будет делить весь ряд выборки на две равные части "верхние" и "нижние".
5
В теории вероятности среднее значение случайной величины не что иное как математическое ожидание. Если у вас дискретное распределение, то математическое ожидание вычисляется по формуле (1), а если непрерывное, но по формуле (2)

Источники:
- среднее взвешенное значение