Инструкция
1
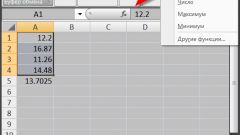
Наиболее распространенной в расчетах является простая средняя величина. Ее вы можете легко найти, если имеется совокупность из двух и более статистических показателей, расположенных в произвольном порядке. Средняя арифметическая простая определяется как отношение суммы индивидуальных значений признака к количеству признаков в совокупности: Хср = ?хi/n.
2
Если объем совокупности большой и представляет собой ряд распределения, то при расчете необходимо использовать среднюю арифметическую взвешенную. Таким способом можно определить, например, среднюю цену за единицу продукции: общую стоимость продукции (произведение количества каждого ее вида на цену) делят на совокупный объем продукции: Хср = ?хi*fi/?fi. Иными словами средняя арифметическая взвешенная определяется как отношение суммы произведений значения признака и частоты повторения данного признака к сумме частот всех признаков. Она используется в случаях, когда варианты исследуемой совокупности встречаются неодинаковое число раз.
3
В некоторых случаях необходимо применять в расчетах среднюю гармоническую. Она используется, когда известны индивидуальные значения признака х и произведение fx, а значение f не известно: Хср = ?wi/?(wi/хi), где wi = хi*fi. Если индивидуальные значения признака встречаются по одному разу (все wi =1), применяется средняя гармоническая простая: Хср = N/?(wi/хi).
4
Дисперсию вы можете посчитать следующим образом: Д = ?(Х-Хср)^2/N, иными словами дисперсия – это средний квадрат отклонения от среднего арифметического значения. Существует еще один способ расчета данного показателя: Д = (Х^2)ср – (Хср)^2. Дисперсию трудно интерпретировать содержательно. Однако квадратный корень из нее характеризует стандартное отклонение. Он отражает среднее отклонение признака от среднего значения выборки.