Существует несколько систем счисления чисел. Так, привычное десятичное число можно представить, например, в виде перебора двоичных символов – это будет двоичная кодировка числа. В восьмеричной системе с основанием 8 число записывается набором цифр от 0 до 7. Но наибольшее распространение имеет шестнадцатеричная система счисления, или система с основанием 16. Для записи числа здесь берутся цифры от 0 до 9 и буквы латиницы от A до F. Перевести десятичное число в его шестнадцатеричную форму можно с помощью таблицы соответствия. А число больше 15 переводится простым разложением по степеням, повтором операции деления на основание 16.
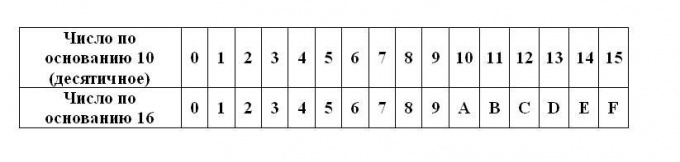
Запишите исходное десятичное число. Если число меньше или равно 15, то для его записи в шестнадцатеричной форме воспользуйтесь таблицей соответствия. Цифры старше 9 заменяются буквенным обозначением, так 10 соответствует букве A с основанием 16, а 15 – букве F.
2
Если число больше 15, для перевода в шестнадцатеричное представление поделите его на 16. Выделите остаток от деления.
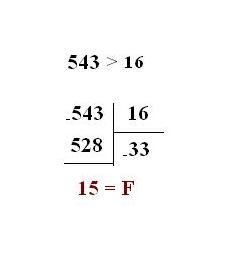
3
Проверьте полученное частное, не меньше ли оно 16. Если частное больше или равно 16, поделите частное также на 16. Выделите остаток деления. Делите получаемые результаты на 16 столько раз, сколько это будет необходимо для получения частного меньше 16. Если частное получилось меньше 16, выделите его тоже, как остаток.
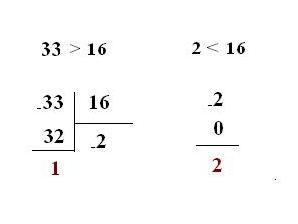
4
Запишите полученные остатки, начиная с последнего числа. Остаток с числом свыше 9 замените по таблице соответствия на букву шестнадцатеричной системы. Полученная запись является шестнадцатеричным представлением исходного десятичного числа.
Полезный совет
Аналогичным образом с помощью деления на основание 8 или 2 можно любое число в десятичном представлении записать в восьмеричной и двоичной системе счисления.
