Вам понадобится
- - бумага;
- - ручка.
Инструкция
1
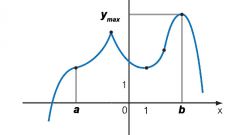
Известно, что для возрастающей функции y=f(x) ее производная f’(x)>0 и соответственно f’(x)
2
Пример: найдите промежутки монотонности y=(x^3)/(4-x^2). Решение. Функция определена на всей числовой оси, кроме х=2 и х=-2. Корме того она нечетна. Действительно, f(-x)=((-x)^3)/(4-(-x)^2)= -(x^3)/(4-x^2)=f(-x). Это означает, что f(x) симметрична относительно начала координат. Поэтому исследование поведение функции можно совершить только для положительных значений х, а затем достроить отрицательную ветвь симметрично положительной.y’=(3(x^2)(4-x^2)+2x(x^3))/((4-x^2)^2)=(x^2)(12-x^2)/((4-x^2)^2).y’ - не существует при x=2 и x=-2, но при этом не существует и сама функция.
3
Теперь необходимо найти интервалы монотонности функции. Для этого следует решить неравенство: (x^2)(12-x^2)/((4-x^2)^2)>0 или (x^2)(x-2sqrt3)(x+2sqrt3)((x-2)^2)((x+2)^2))0. Используйте метод интервалов, при решении неравенства. Тогда получится (см. рис.1).
4
Далее рассмотрите поведение функции на интервалах монотонности, присоединяя сюда все сведения из области отрицательных значений числовой оси (в силу симметрии все сведения там обратны, в том числе и по знаку).f’(x)>0 при –∞
5
Пример 2. Найти промежутки возрастания и убывания функции y=x+lnx/x.Решение. Область определения функции – x>0.y’=1+(1-lnx)/(x^2)=(x^2+1-lnx)/(x^2). Знак производной при x>0 полностью определяется скобкой (x^2+1-lnx). Так как x^2+1>lnx, то y’>0. Таким образом, функция возрастает на всей своей области определения.
6
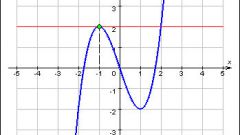
Пример 3. Найти интервалы монотонности функции y’=x^4-2x^2-5.Решение. y’=4x^3-4x=4x(x^2-1)=4x(x-1)(x+1). Применяя метод интервалов (см. рис.2), необходимо найти промежутки положительных и отрицательных значений производной. Используя метод интервалов, вы сможете быстро определить, что на промежутках x0 функция возрастает.