Инструкция
1
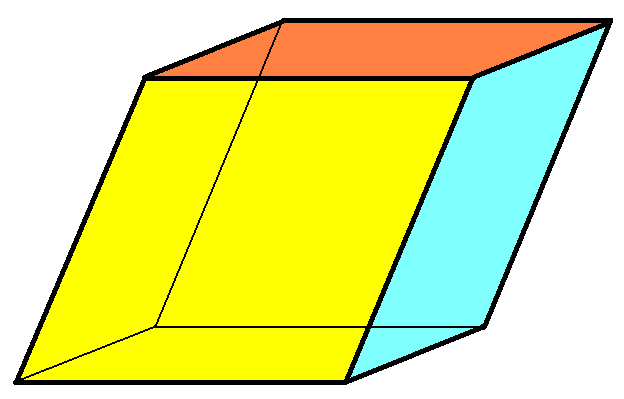
Как было сказано выше, основанием параллелепипеда является параллелограмм. Для того, чтобы найти объем параллелепипеда, необходимо выяснить площадь того параллелограмма, который лежит в основании. Для это, в зависимости от известных данных, существуют несколько формул:

S = a*h, где а - сторона параллелограмма, h - высота, проведенная к этой стороне;м

S = a*b*sinα, где, a и b - стороны параллелограмма, α - угол между данными сторонами.

Пример 1: Дан параллелограмм, у которого одна из сторон равна 15 см, длина высоты, проведенной к данной стороне, 10 см. Тогда, чтобы найти площадь данной фигуры на плоскости, применяется первая из двух указанных выше формул:

S = 10*15 = 150 см²

Ответ: Площадь параллелограмма составляет 150 см²
2
Теперь, разобравшись с тем, как находить площадь параллелограмма, можно приступить к нахождению объема параллелепипеда. Объем параллелепипеда можно найти по формуле:

V = S*h, где h - высота данного параллелепипеда, S - площадь его основания, нахождение которой было рассмотрено выше.

Можно рассмотреть пример, который бы включал решенную выше задачу:

Площадь основания параллелограмма 150 см², его высота, допустим, 40 см, требуется найти объем данного параллелепипеда. Решается эта задача при помощи данной выше формулы:

V = 150*40 = 6000 см³
3
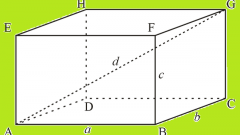
Одной из разновидностей параллелепипеда является прямоугольный параллелепипед, у которого боковые грани и основание являются прямоугольниками. У этой фигуры найти объем еще проще, чем у обычного прямого параллелепипеда, нахождение объема которого было рассмотрено выше:

V = a*b*c, где a, b, c, - это длина, ширина и высота данного параллелепипеда.

Пример: У прямоугольного параллелепипеда длина и ширина основания составляют 12 см и 14 см, длина боковой грани (высоты) 14 см, требуется вычислить объем фигуры. Решается задача таким вот образом:

V = 12*14*14 = 2352 см³

Ответ: объем прямоугольного параллелепипеда равен 2352 см³