Как определить частоту сигнала

Известно большое число измерителей частоты, в том числе и электромагнитных колебаний. Тем не менее, вопрос поставлен, и это означает, что читателя больше интересует принцип, положенный в основу, например, радиоизмерений. Ответ базируется на статистической теории радиотехнических устройств и посвящен оптимальному измерению частоты радиоимпульса.

Инструкция

1. Для получения алгоритма функционирования оптимальных измерителей, прежде всего, необходимо выбрать критерий оптимальности. Любое измерение случайно. Полное вероятностное описание случайной величины дает такой ее закон распределения, как плотность вероятности. В данном случае это апостериорная плотность, то есть такая, которая становится известной после измерения (опыта). В рассматриваемой задаче измерению подлежит частота - один из параметров радиоимпульса. Кроме того, в силу имеющейся случайности, речь может идти только о приблизительном значении параметра, то есть о его оценке.
2. В рассматриваемом случае (когда не проводится повторное измерение) рекомендуется использовать оценку, оптимальную по методу апостериорной плотности вероятности. Фактически это мода (Мо). Пусть на приемную сторону пришла реализация вида y(t)=Acosωt+n(t), где n(t) гауссовский белый шум с нулевым средним и известными характеристиками; Acosωt – радиоимпульс с постоянной амплитудой А, длительностью τ и нулевой начальной фазой. Для выяснения структуры апостериорного распределения используйте байесовский подход к решению задачи. Рассмотрите совместную плотность вероятности ξ(у,ω)=ξ(у)ξ(ω|y)=ξ(ω)ξ(y|ω). Тогда апостериорная плотность вероятности частоты ξ(ω|y)=(1/ξ(у))ξ(ω)ξ(y|ω). Здесь ξ(у) не зависит от ω явно и, поэтому априорная плотность ξ(ω) в пределах апостериорной будет практически равномерна. Нам следует следить за максимумом распределения. Значит ξ(ω|y)=kξ(y|ω).
3. Условная плотность вероятности ξ(y|ω) - распределение значений принятого сигнала, при условии, что частота радиоимпульса приняла конкретное значение, то есть прямая зависимость отсутствует и это целое семейство распределений. Тем не менее, такое распределение, называемое функцией правдоподобия, показывает - какие значения частоты наиболее правдоподобны, при фиксированном значении принятой реализации у. Кстати, это и не функция вовсе, а функционал, так как переменная целая кривая y(t).
4. Далее все просто. Имеющееся распределение гауссовское (так как использована модель гауссовского белого шума). Среднее значение (или математическое ожидание) М[y|ω] = Acosωt=Mo[ω]. Прочие параметры распределения Гаусса отнесите к постоянной С, и вспомните, что присутствующая в формуле этого распределения экспонента монотонна (значит ее максимум совпадет с максимумом показателя экспоненты). Кроме того частота – не энергетический параметр, а энергия сигнала является интегралом его квадрата. Поэтому вместо полного показателя экспоненты функционала правдоподобия, включающего -С1∫[0,τ][(y-Acosωt)^2] dt (интеграл от 0 до τ) остается анализ на максимум взаимно корреляционного интеграла η(ω). Его запись и соответствующая структурная схема измерения приведены на рисунке 1, где показан результат при некоторой частоте опорного сигнала ωi.
   
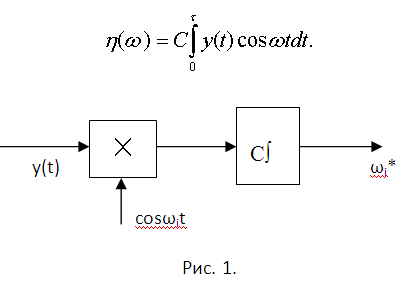
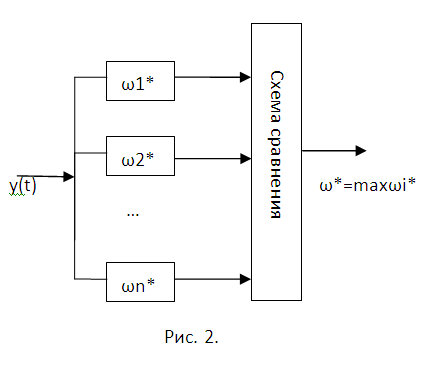
5. Для окончательного построения измерителя следует выяснить, какая точность (погрешность) вас устроит. Далее разбейте весь диапазон предполагаемых результатов на сопоставимое число отдельных частот ωi и используйте для измерений многоканальную схему, где выбор ответа обуславливает сигнал с максимальным выходным напряжением. Такая схема представлена на рисунке 2. Каждая отдельная «линейка» на ней соответствует рис. 1.