Как определять исходную концентрацию вещества

Вещества, вступающие в химическую реакцию, претерпевают изменения состава и строения, превращаясь в продукты реакции. Концентрация исходных веществ уменьшается вплоть до нуля, если реакция идет до конца. Но может протекать обратная реакция, когда продукты распадаются на исходные вещества. В таком случае устанавливается равновесие, когда скорость прямой и обратной реакции становится одинаковой. Разумеется, равновесные концентрации веществ будут меньше исходных.

Инструкция

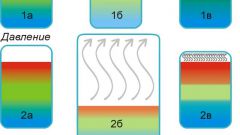
1. Произошла химическая реакция по схеме: А + 2Б = В. Исходные вещества и продукт реакции – газы. В какой-то момент установилось равновесие, то есть, скорость прямой реакции (А + 2Б = В) сравнялась со скоростью обратной (В = А + 2Б). Известно, что равновесная концентрация вещества А равна 0,12 моль/литр, элемента Б – 0,24 моль/литр, а вещества В – 0,432 моль/литр. Требуется определить исходные концентрации А и Б.
2. Изучите схему химического взаимодействия. Из нее следует, что один моль продукта (элемента В) образовывался из одного моля вещества А и двух молей вещества Б. Если в одном литре реакционного объема образовывалось 0,432 моля элемента В (по условиям задачи), то, соответственно, одновременно расходовалось 0,432 моля вещества А и 0,864 моля элемента Б.
3. Вам известны равновесные концентрации исходных веществ: [A] = 0,12 моль/литр, [Б] = 0,24 моль/литр. Прибавив к этим величинам те, которые были израсходованы в ходе реакции, вы получите величины исходных концентраций: [A]0 = 0,12 + 0,432 = 0,552 моль/литр; [Б]0 = 0,24 + 0,864 = 1,104 моль/литр.
4. Также вы можете определить исходные концентрации веществ с помощью константы равновесия (Кр) - отношения произведений равновесных концентраций продуктов реакции к произведению равновесных концентраций исходных веществ. Константа равновесия рассчитывается по формуле: Кр = [C]n [D]m /([A]0x[B]0y), где [C] и [D] – равновесные концентрации продуктов реакции С и D; n, m – их коэффициенты. Соответственно, [A]0, [В]0 – равновесные концентрации элементов, вступающих в реакцию; x,y – их коэффициенты.
5. Зная точную схему протекающей реакции, равновесную концентрацию хотя бы одного продукта и исходного вещества, а также величину константы равновесия, можно записать условия этой задачи в виде системы двух уравнений с двумя неизвестными.