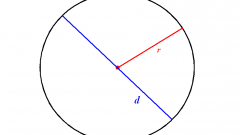
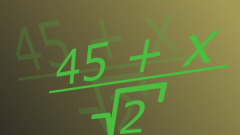Согласно понятиям геометрии, если в двух отрезках содержится какое-то количество одинаковых значений, то они соизмеримы. Например, разные стороны прямоугольника соизмеримы. Но вот сторона квадрата и его диагональ не являются соизмеримыми. Они не имеют общей меры, в которой их можно было бы выразить. Иррациональные числа относятся к неявно выраженным. Они несоизмеримы с рациональными числами.К рациональным относятся целые, дробные, а также конечные и периодические десятичные числа. Они являются соизмеримыми единице. Бесконечные десятичные непериодические дроби называют иррациональными, с единицей они несоизмеримы. Но может быть указан способ получения такого числа, тогда оно считается заданным точно. С помощью такого способа можно найти любое количество знаков после запятой у иррационального числа, это называется вычислить число с определенной точностью, которая как раз и задается количеством требуемых к вычислению знаков.Свойства иррациональных чисел во многом схожи со свойствами рациональных. Например, сравниваются они одинаково, над ними возможно производить те же самые арифметические действия, они могут быть положительными или отрицательными. Умножение иррационального числа на ноль, точно так же как и рационального, дает ноль.Если операция производится над двумя числами, одно из которых рациональное, а другое иррациональное, то принято по возможности не использовать приближенное значение, а брать точным образом заданное число (например, в виде недесятичной дроби).Считается, что первым концепцию иррациональных чисел открыл Гиппас из Метапонта, живший примерно в VI в. до н.э. Он был последователем пифагорейской школы. Свое открытие Гиппас совершил во время морского похода, находясь на корабле. Согласно легенде, когда он рассказал другим пифагорейцам об иррациональных числах, предоставив доказательство их существования, те выслушали его и признали его выкладки правильными. Тем не менее, открытие Гиппаса настолько шокировало их, что он был выброшен за борт за то, что создал нечто, опровергающее центральную пифагорейскую доктрину о том, что все во вселенной может быть сведено к целым числам и их отношениям.