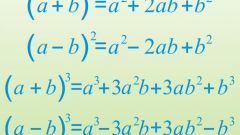Инструкция
1
Выберите из перемножаемых многочленов тот, который содержит меньшее число составных частей, и раскройте его скобки. Выбирать наиболее простой не обязательно, так как в операции умножения все многочлены-множители равнозначны, но при работе со сложными алгебраическими выражениями это лучше сделать, чтобы усложнять результирующее выражение постепенно. Например, при умножении многочленов (7x+3x?-15) и (х-5) раскройте скобки составленного из двух членов второго выражения: (7*x+3*x?-15)*(х-5) = х*(7*x+3*x?-15) - 5*(7*x+3*x?-15).
2
Перемножьте каждый член многочлена, скобки которого были раскрыты на предыдущем шаге, на каждый оставшийся внутри скобок член другого многочлена, не забыв проследить за знаками полученных частей выражения. Для примера из первого шага эти действия можно записать так: (7*x+3*x?-15)*(х-5) = х*(7*x+3*x?-15) - 5*(7*x+3*x?-15) = 7*x?+3*x?-15*х - 35*x-15*x?+75.
3
Сократите полученное в результате двух предыдущих шагов выражение. В использованном выше примере на этом шаге вся запись должна выглядеть так: (7*x+3*x?-15)*(х-5) = х*(7*x+3*x?-15) - 5*(7*x+3*x?-15) = 7*x?+3*x?-15*х - 35*x-15*x?+75 = 3*x?-8*x?-50*x+75.
4
Запомните формулы для наиболее часто встречающихся при умножении комбинаций многочленов - это рекомендуется делать еще в школьном курсе алгебры. Например, это относится к формулам умножения многочлена вида (x+y) на самого себя, то есть возведение его в квадрат (x+y)?=x?+2*x*y+y?, произведения суммы двух переменных на их разность (x+y)*(x-y)=x?-y?, аналогичных формул для третьих степеней (x+y)?=x?+3*x?*y+3x*y?+y? и (x+y)*(x?-x*y+y?)=x?+y? и некоторых других.
Видео по теме