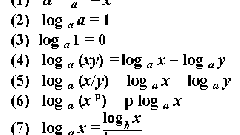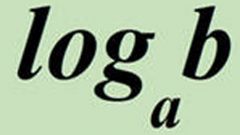Инструкция
1
Логарифм числа x по основанию a будем обозначать loga(x). Например, log2(8) — логарифм числа 8 по основанию 2. Он равен 3, потому что 2^3 = 8.
2
Логарифм определен только для положительных чисел. Отрицательные числа и ноль не имеют логарифмов вне зависимости от основания. При этом сам логарифм может быть любым числом.
3
Основанием логарифма может служить любое положительное число, кроме единицы. Однако на практике чаще всего используются два основания. Логарифмы по основанию 10 называются десятичными и обозначаются lg(x). Десятичные логарифмы чаще всего встречаются в практических вычислениях.
4
Второе популярное основание для логарифмов — иррациональное трансцендентное число e = 2,71828… Логарифм по основанию e называется натуральным и обозначается ln(x). Функции e^x и ln(x) обладают особыми свойствами, важными для дифференциального и интегрального исчисления, поэтому натуральные логарифмы чаще используются в математическом анализе.
5
Логарифм произведения двух чисел равен сумме логарифмов этих чисел по тому же основанию: loga(x*y) = loga(x) + loga(y). Например, log2(256) = log2(32) + log2(8) = 8.Логарифм частного двух чисел равен разности их логарифмов: loga(x/y) = loga(x) - loga(y).
6
Чтобы найти логарифм числа, возведенного в степень, нужно логарифм самого числа умножить на показатель степени: loga(x^n) = n*loga(x). При этом показатель степени может быть любым числом — положительным, отрицательным, нулем, целым или дробным.Поскольку x^0 = 1 для любого x, то loga(1) = 0 для любого a.
7
Логарифм заменяет умножение сложением, возведение в степень умножением, а извлечение корня делением. Поэтому в отсутствие вычислительной техники логарифмические таблицы заметно упрощают расчеты.Чтобы найти логарифм числа, не входящего в таблицу, его нужно представить в виде произведения двух или более чисел, логарифмы которых есть в таблице, и найти окончательный результат, сложив эти логарифмы.
8
Достаточно простой способ вычислить натуральный логарифм — воспользоваться разложением этой функции в степенной ряд:ln(1 + x) = x - (x^2)/2 + (x^3)/3 - (x^4)/4 + … + ((-1)^(n + 1))*((x^n)/n).Этот ряд дает значения ln(1 + x) для -1 < x ≤1. Иными словами, так можно вычислить натуральные логарифмы чисел от 0 (но не включая 0) до 2. Натуральные логарифмы чисел за пределами этого ряда можно найти путем суммирования найденных, пользуясь тем, что логарифм произведения равен сумме логарифмов. В частности ln(2x) = ln(x) + ln (2).
9
Для практических вычислений иногда бывает удобно перейти от натуральных логарифмов к десятичным. Любой переход от одного основания логарифмов к другому совершается по формуле:logb(x) = loga(x)/loga(b).Таким образом, log10(x) = ln(x)/ln(10).