Инструкция
1
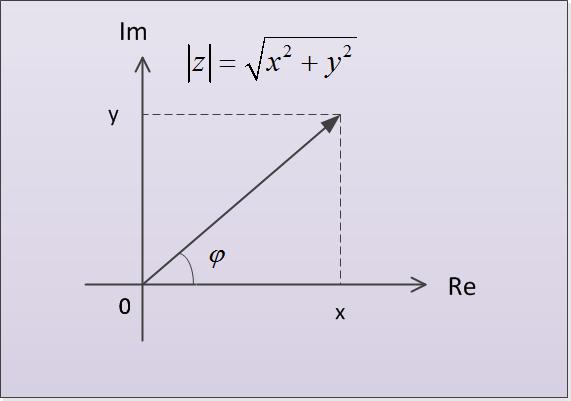
Плоскость, на которой представляют комплексные числа, называется комплексной. На этой плоскости горизонтальную ось занимают вещественные числа (x), а вертикальную ось – мнимые числа (y). На такой плоскости число задается двумя координатами z = {x, y}. В полярной системе координат координатами точки являются модуль и аргумент. Модулем называют расстояние |z| от точки до начала координат. Аргументом называют угол ϕ между вектором, соединяющим точку и начало координат и горизонтальной осью системы координат (см. рисунок).
2
Из рисунка видно, что модуль комплексного числа z = x + i * y находится по теореме Пифагора: |z| = √ (x^2 + y^2). Далее аргумент числа z находится как острый угол треугольника – через значения тригонометрических функций sin, cos, tg:sin ϕ = y / √ (x^2 + y^2),
cos ϕ = x / √ (x^2 + y^2),
tg ϕ = y / x.
cos ϕ = x / √ (x^2 + y^2),
tg ϕ = y / x.
3
Например, пусть дано число z = 5 * (1 + √3 * i). Первым делом выделите вещественную и мнимую части: z = 5 +5 * √3 * i. Получается, что вещественная часть x = 5, а мнимая часть y = 5 * √3. Вычислите модуль числа: |z| = √(25 + 75) = √100 =10. Далее найдите синус угла ϕ: sin ϕ = 5 / 10 = 1 / 2. Отсюда получается аргумент числа z равен 30°.
4
Пример 2. Пусть дано число z = 5 * i. По рисунку видно, что угол ϕ = 90°. Проверьте это значение по формуле, приведенной выше. Запишите координаты данного числа на комплексной плоскости: z = {0, 5}. Модуль числа |z| = 5. Тангенс угла tg ϕ = 5 / 5 = 1. Отсюда следует, что ϕ = 90°.
5
Пример 3. Пусть необходимо найти аргумент суммы двух комплексных чисел z1 = 2 + 3 * i, z2 = 1 + 6 * i. По правилам сложения складываете эти два комплексных числа: z = z1 + z2 = (2 + 1) + (3 + 6) * i = 3 + 9 * i. Далее по приведенной выше схеме рассчитываете аргумент: tg ϕ = 9 / 3 = 3.
Обратите внимание
Если число z = 0, то значение аргумента для него не определено.
Полезный совет
Значение аргумента комплексного числа определяется с точностью до 2 * π * k, где k – любое целое число. Значение аргумента ϕ такое, что –π < ϕ ≤ π называется главным значением аргумента.
Источники:
- как находить аргументы в текстах