Вам понадобится
- - лист бумаги;
- - циркуль;
- - линейка.
Инструкция
1
Научитесь использовать правило золотого сечения при делении отрезка. Золотое сечение для отрезка означает его деление на две неравные части в определенной пропорции. Меньшая часть так относится к большей, как большая ко всей длине. Обозначив длину отрезка как L, его большую и меньшую часть, соответственно, как a и b, вы получите соотношение b:а=а:L. Деление отрезка проводится с помощью линейки и циркуля.
2
Начертите отрезок произвольной длины. Для удобства расположите его горизонтально. Обозначьте его конечные точки как А и В. Измерьте расстояние между ними.
3
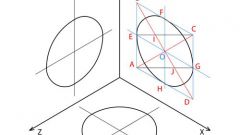
Разделите длину отрезка на 2. Из точки В проведите к нему перпендикуляр. Отложите на нем расстояние, равное половине длины исходного отрезка. Поставьте точку С. Соедините эту новую точку с точкой А. У вас получится прямоугольный треугольник.
4
От точки С по гипотенузе АС отмерьте отрезок, равный ВС, и поставьте точку D. От точки А по прямой АВ отложите величину этого нового отрезка и поставьте точку Е. Она и делит первоначальный отрезок по правилу золотого сечения.
5
Можно найти численное значение этой пропорции. Оно исчисляется по формуле х2-х-1=0. Найдите корни этого уравнения х1 и х2. Их значения равны сумме или разности единицы и квадратного корня из пяти, деленного на 2. То есть х1=1+√5)/2, а х2=(1-√5)/2. В итоге получается бесконечная иррациональная дробь.
6
Для практического применения обычно используют приблизительное соотношение. Допустим, что целый отрезок АВ равен единице. Тогда отрезок АЕ будет приблизительно равен 0,62, а отрезок ЕВ — 0,38.
Видео по теме
Обратите внимание
В конце прошлого века было введено понятие второго золотого сечения. В этом случае первоначальный отрезок делится по правилам золотого сечения. Из точки деления С проведите к отрезку перпендикуляр и отложите на нем расстояние, равное АВ. Полученную точку D соедините с точкой А. Из угла АСD проведите биссектрису до ее пересечения с линией АD. Поставьте точку Е. Она делит отрезок примерно в соотношении 44:56.
Источники:
- Золотое сечение
- построение золотого сечения